[Машинное обучение, Финансы в IT] БСД для финансистов – хорошо, но Диаграммы влияния – лучше
Автор
Сообщение
news_bot ®
Стаж: 7 лет 8 месяцев
Сообщений: 27286
Разбирая примеры с использованием Байесовских сетей доверия (БСД), мы показали, как с их помощью формируется или принимается некое решение инвестора или другого лица, принимающего решения (ЛПР). Однако в чистом виде БСД могут быть лишь основой для принятия решений. Инструментом же, созданным специально для этого являются Диаграммы влияния (Influence Diagrams). Так называют разновидность байесовских сетей, в которой, помимо уже знакомых нам узлов неопределенностей (случайных переменных) используют еще два вида узлов:- узлы решений, которые должны быть приняты. Если дуга (стрелка) направлена к узлу решений, это означает, что узел в начале такой дуги должен быть полностью определён к моменту принятия решения. Поэтому такие дуги часто называют информационными;- узлы полезностей, представляющие возможные значения (ценность, полезность) результатов. Родителями обычного узла полезности могут быть только узлы неопределенностей и узлы решений. Однако иногда строят модели с особыми «сверхценными» узлами полезности, родителями которых являются обычные узлы полезностей. Сверхценные узлы полезности представляют взвешенную сумму результатов обычных узлов полезности.Диаграммы влияния, в отличие от обычных БСД, позволяют определять ожидаемую полезность всех альтернативных решений, а затем выбирать альтернативу с наибольшей ожидаемой полезностью. На блок-схемах узлы случайных переменных обычно изображают окружностями (овалами), узлы решений – прямоугольниками, а узлы полезностей – ромбами. Программа Netica, которую мы использовали в предыдущих примерах, полностью приспособлена для постройки диаграмм влияния.Итак, в предыдущих статьях о БСД мы уже разобрали европейский опцион колл на акцию, а затем и саму акцию. Из этих «кирпичиков» далее построим Диаграмму влияния для анализа альтернативных решений инвестора с горизонтом 1 месяц. В этом примере инвестор является «крупным игроком», решение которого может даже краткосрочно повлиять на курс интересующей его акции. В частности, он планирует покупку 10 тыс. акций компании Аа по цене 10 руб. за штуку. Инвестор считает, что фондовый индекс РТС (RTSI) существенно влияет на курс данной акции. Кроме того, основываясь на собственном опыте и имеющейся информации, инвестор полагает, что к концу месяца индекс РТС вырастет, при этом акция Аа, скорее всего, будет стоить 5 или 20 руб.Альтернативным выбором инвестора является приобретение за 100 тыс. руб. европейского опциона колл на акции Аа. Опцион дает право на покупку 50 тыс. акций Аа в конце месяца по цене 15 руб. за штуку.Для анализа решений инвестора построим диаграмму влияния, включающую четыре узла (Рис. 1):- узел случайной переменной цены акции Аа в конце месяца. Узел представляет две несовместные гипотезы о будущей цене акции, выдвинутые инвестором;- узел случайной переменной величины индекса РТС (родительский узел);- узел Решение, представляющий два альтернативных варианта решения, которые может принять инвестор, а именно: купить 10 тыс. акций Аа, или приобрести опцион стоимостью 100 тыс. руб. на покупку 50 тыс. акций Аа в конце месяца.- узел полезности U, представляющий ожидаемый результат инвестирования.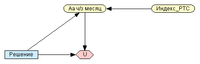
Рис. 1. Исходная диаграмма.Прежде всего, отметим здесь, что наличие стрелок от узла акции Аа и от узла Решения к узлу полезности U говорит нам о том, что и курс акции и решение инвестора влияют на ожидаемый результат инвестирования. Стрелка от узла индекса РТС к акции подтверждает его влияние на текущий и будущий на курс акции. Наконец, стрелка от узла Решение к узлу акции указывает на возможное влияние решения инвестора на курс данной акции, поскольку сумма его предполагаемой покупки достаточно велика.Следующий шаг – заполнение таблиц вероятностей. Узел РТС является родительским, поэтому таблицу безусловных вероятностей (ТБВ, Таблица 1) его состояния заполняем исходя из того, что инвестору известно состояние рынка, и он, основываясь на собственном опыте, ожидает, что индекс РТС с вероятностью 60% к концу месяца достигнет уровня 1400 единиц, или с вероятностью 40% – уровня 1300 единиц.Таблица 1. ТБВ для узла РТС.№Индекс РТСВероятность, %11400602130040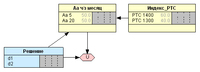
Рис. 2. Диаграмма влияния до инициализации.До инициализации модели в программе Netica стержневые диаграммы на узлах переменных не высвечиваются (Рис. 2), т.к. это не имеет смысла, пока не заполнены таблицы условных вероятностей (ТУВ). Как обычно, в ТУВ узла акции мы должны «перебрать» все возможные сочетания состояний родительского узла и данного узла, исходя из предположений инвестора (см. Табл. 2).В этой таблице мы видим, что, суммируя свои знания, опыт и рыночную информацию, инвестор предполагает, что при достижении индексом РТС значения 1400 единиц (1-я и 3-я строки ТУВ) курс акции Аа с большей вероятностью достигнет значения 20 руб. (80% при выборе акции, и 70% при выборе опциона). Если индекс дойдет только до 1300 единиц, то ожидания инвестора не определены при выборе акции (2-я строка ТУВ – 50/50), и немного сдвинуты в противоположном направлении при выборе опциона (4-я строка ТУВ).Таблица 2. ТУВ для узла акции.№РешениеРТСВероятность цены акции, %А5 = 5 руб.А5 = 20 руб.1d1140020802d1130050503d2140030704d213006040Завершающий этап – заполнение таблицы случайных значений полезности (Табл. 3). В ней будет всего четыре возможных значения результата инвестирования. Здесь отметим для себя, что в случае покупки опциона (d2) и курса Аа в конце месяца 5 руб. инвестор не получает ничего, но при курсе 20 руб. он получит 250 тыс. руб.Таблица 3. Состояния узла полезности.РешениеU, руб.АСК = 5 руб.АСК = 20 руб.d150000200000d20250000После заполнения всех таблиц инициализируем диаграмму, и только после этого получаем действующую модель решений нашего инвестора (Рис. 3). В таблице узла решений видим значения ожидаемых результатов инвестирования в денежном выражении: 152 тыс. руб. для решения d1, и 145 тыс. руб. для решения d2. Попробуем и в этом примере проверить машину.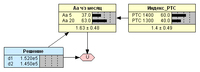
Рис. 3. Модель решений инвестора.Ожидаемое значение результата покупки акции (решение d1) с учетом заданных вероятностей и каждого значения индекса РТС составит:Е(U1) = 0,2 · 50 тыс. руб. + 0,8 · 200 тыс. руб. = 170 тыс. руб. (РТС =1400)Е(U2) = 0,5 · 50 тыс. руб. + 0,5 · 200 тыс. руб. = 125 тыс. руб. (РТС =1300)Следовательно, ожидаемый результат в случае покупки акции:Е(d1) = 0,6 · 170 тыс. руб. + 0,4 · 125 тыс. руб. = 152 тыс. руб.По такому же принципу считаем ожидаемый результат в случае покупки опциона (решение d2):Е(U3) = 0,3 · 0 + 0,7 · 250 тыс. руб. = 175 тыс. руб. (РТС =1400)Е(U4) = 0,6 · 0 + 0,4 · 250 тыс. руб. = 100 тыс. руб. (РТС =1300)Следовательно, ожидаемый результат в случае покупки опциона составит:Е(d2) = 0,6 · 175 тыс. руб. + 0,4 · 100 тыс. руб. = 145 тыс. руб.Как видим, всё совпало. Инвестору остается выбрать альтернативу с наибольшей ожидаемой полезностью, поэтому его решением должна быть покупка акции, т.к. это решение дает максимальное ожидаемое значение результата инвестирования в условиях неопределенности:Е(Решение) = max (152 тыс. руб.; 145 тыс. руб.) = 152 тыс. руб.Для того чтобы продемонстрировать правильность решения кликаем мышью в строке d1 и убеждаемся, что машина оставит именно такой результат в таблице узла Решение (см. Рис. 4). При этом в строке решения d2 будет выведен нуль.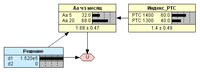
Рис. 4. Вывод окончательного решения.Для того чтобы проверить теперь уже наши расчеты, сделаем некоторые вероятностные выводы с помощью построенной модели. Например, убедимся, что при достижении индексом РТС значения 1400 (Рис. 5) модель выдает точно такие же ожидаемые результаты, которые мы получили выше, когда проверяли результаты в отдельности для случаев выбора акции или опциона.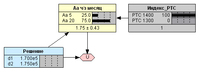
Рис. 5. Прямой вероятностный вывод (РТС = 1400).Далее сделаем то же самое при достижении индексом РТС значения 1300 (Рис. 6), и также сверим результат.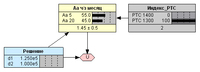
Рис.6. Прямой вероятностный вывод (РТС = 1300).Далее усложним вывод, и зададим состояние, при котором индекс РТС достиг значения 1400, а акция Аа достигла курса 20 руб. (Рис. 7). Значения полученных результатов для такого состояния проверяем по Таблице 3.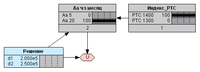
Рис. 7. Прямой вероятностный вывод (РТС = 1400; Аа = 20 руб.).Далее проверим, что могло бы произойти, если бы курс акции Аа не достиг значения 20 руб. (Рис. 8), и получаем подтверждение того, что в этом случае выбор опциона (d2) дал бы нулевой результат при любом значении индекса РТС.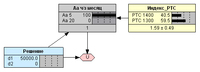
Рис. 8. Прямой вероятностный вывод (Аа = 5 руб.).Таким образом, мы убеждаемся, что даже довольно простая диаграмма влияния позволяет проводить множество интересных вероятностных выводов на построенной модели принятия решений. Опыт показывает, что диаграммы влияния пригодны для задач моделирования реальных опционов, синтетических инструментов на базе теории паритета финансовых опционов, анализа различных арбитражных возможностей, т.е. там, где неопределенностей особенно много.В данном простом примере всю таблицу полезности мы рассчитали и заполнили вручную. Однако в программах-редакторах БСД, и в Netica в частности предусмотрено заполнении таких таблиц программным путём, если известны необходимые для этого зависимости. Такие примеры мы тоже рассмотрим.
===========
Источник:
habr.com
===========
Похожие новости:
- [Python, Машинное обучение, Разработка на Raspberry Pi, TensorFlow] Как на Raspberry Pi запустить модель ML и сэкономить пространство одноплатника (перевод)
- [Разработка игр, Машинное обучение, Искусственный интеллект] Волк, предпочитающий самоубийство съедению овцы (перевод)
- [Облачные сервисы, Софт, Финансы в IT, IT-компании] Microsoft c 1 октября повысит рублёвые цены на коммерческое ПО и облачные сервисы на 15,2%
- [Open source, Программирование, GitHub, Машинное обучение, IT-компании] GitHub признался, что использовал весь публичный код для обучения Copilot без учёта типа лицензии
- [Законодательство в IT, Карьера в IT-индустрии, Финансы в IT] Минфин опроверг планы изменить систему страховых взносов
- [Data Mining, Визуализация данных, Машинное обучение, Data Engineering] Курс «Анализ данных и машинное обучение в MATLAB»
- [Python, Алгоритмы, Big Data, Машинное обучение, Искусственный интеллект] Data Phoenix Digest — 08.07.2021
- [Законодательство в IT, Карьера в IT-индустрии, Финансы в IT] Чиновники предложили повысить страховые взносы с зарплат более 122 тысяч рублей
- [Big Data, Машинное обучение] Google выпускает MLP-Mixer: MLP архитектуру для компьютерного зрения
- [Информационная безопасность, Работа с видео, Машинное обучение, Искусственный интеллект] Бельгийский политический активист научил систему машинного зрения помечать на видео политиков, не слушающих заседание
Теги для поиска: #_mashinnoe_obuchenie (Машинное обучение), #_finansy_v_it (Финансы в IT), #_finansovyj_inzhiniring (финансовый инжиниринг), #_mashinnoe+obuchenie (машинное+обучение), #_bajesovskie_seti (байесовские сети), #_diagrammy_vlijanija (Диаграммы влияния), #_netica, #_mashinnoe_obuchenie (
Машинное обучение
), #_finansy_v_it (
Финансы в IT
)
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 30-Окт 06:23
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 8 месяцев |
|
|
Разбирая примеры с использованием Байесовских сетей доверия (БСД), мы показали, как с их помощью формируется или принимается некое решение инвестора или другого лица, принимающего решения (ЛПР). Однако в чистом виде БСД могут быть лишь основой для принятия решений. Инструментом же, созданным специально для этого являются Диаграммы влияния (Influence Diagrams). Так называют разновидность байесовских сетей, в которой, помимо уже знакомых нам узлов неопределенностей (случайных переменных) используют еще два вида узлов:- узлы решений, которые должны быть приняты. Если дуга (стрелка) направлена к узлу решений, это означает, что узел в начале такой дуги должен быть полностью определён к моменту принятия решения. Поэтому такие дуги часто называют информационными;- узлы полезностей, представляющие возможные значения (ценность, полезность) результатов. Родителями обычного узла полезности могут быть только узлы неопределенностей и узлы решений. Однако иногда строят модели с особыми «сверхценными» узлами полезности, родителями которых являются обычные узлы полезностей. Сверхценные узлы полезности представляют взвешенную сумму результатов обычных узлов полезности.Диаграммы влияния, в отличие от обычных БСД, позволяют определять ожидаемую полезность всех альтернативных решений, а затем выбирать альтернативу с наибольшей ожидаемой полезностью. На блок-схемах узлы случайных переменных обычно изображают окружностями (овалами), узлы решений – прямоугольниками, а узлы полезностей – ромбами. Программа Netica, которую мы использовали в предыдущих примерах, полностью приспособлена для постройки диаграмм влияния.Итак, в предыдущих статьях о БСД мы уже разобрали европейский опцион колл на акцию, а затем и саму акцию. Из этих «кирпичиков» далее построим Диаграмму влияния для анализа альтернативных решений инвестора с горизонтом 1 месяц. В этом примере инвестор является «крупным игроком», решение которого может даже краткосрочно повлиять на курс интересующей его акции. В частности, он планирует покупку 10 тыс. акций компании Аа по цене 10 руб. за штуку. Инвестор считает, что фондовый индекс РТС (RTSI) существенно влияет на курс данной акции. Кроме того, основываясь на собственном опыте и имеющейся информации, инвестор полагает, что к концу месяца индекс РТС вырастет, при этом акция Аа, скорее всего, будет стоить 5 или 20 руб.Альтернативным выбором инвестора является приобретение за 100 тыс. руб. европейского опциона колл на акции Аа. Опцион дает право на покупку 50 тыс. акций Аа в конце месяца по цене 15 руб. за штуку.Для анализа решений инвестора построим диаграмму влияния, включающую четыре узла (Рис. 1):- узел случайной переменной цены акции Аа в конце месяца. Узел представляет две несовместные гипотезы о будущей цене акции, выдвинутые инвестором;- узел случайной переменной величины индекса РТС (родительский узел);- узел Решение, представляющий два альтернативных варианта решения, которые может принять инвестор, а именно: купить 10 тыс. акций Аа, или приобрести опцион стоимостью 100 тыс. руб. на покупку 50 тыс. акций Аа в конце месяца.- узел полезности U, представляющий ожидаемый результат инвестирования.  Рис. 1. Исходная диаграмма.Прежде всего, отметим здесь, что наличие стрелок от узла акции Аа и от узла Решения к узлу полезности U говорит нам о том, что и курс акции и решение инвестора влияют на ожидаемый результат инвестирования. Стрелка от узла индекса РТС к акции подтверждает его влияние на текущий и будущий на курс акции. Наконец, стрелка от узла Решение к узлу акции указывает на возможное влияние решения инвестора на курс данной акции, поскольку сумма его предполагаемой покупки достаточно велика.Следующий шаг – заполнение таблиц вероятностей. Узел РТС является родительским, поэтому таблицу безусловных вероятностей (ТБВ, Таблица 1) его состояния заполняем исходя из того, что инвестору известно состояние рынка, и он, основываясь на собственном опыте, ожидает, что индекс РТС с вероятностью 60% к концу месяца достигнет уровня 1400 единиц, или с вероятностью 40% – уровня 1300 единиц.Таблица 1. ТБВ для узла РТС.№Индекс РТСВероятность, %11400602130040  Рис. 2. Диаграмма влияния до инициализации.До инициализации модели в программе Netica стержневые диаграммы на узлах переменных не высвечиваются (Рис. 2), т.к. это не имеет смысла, пока не заполнены таблицы условных вероятностей (ТУВ). Как обычно, в ТУВ узла акции мы должны «перебрать» все возможные сочетания состояний родительского узла и данного узла, исходя из предположений инвестора (см. Табл. 2).В этой таблице мы видим, что, суммируя свои знания, опыт и рыночную информацию, инвестор предполагает, что при достижении индексом РТС значения 1400 единиц (1-я и 3-я строки ТУВ) курс акции Аа с большей вероятностью достигнет значения 20 руб. (80% при выборе акции, и 70% при выборе опциона). Если индекс дойдет только до 1300 единиц, то ожидания инвестора не определены при выборе акции (2-я строка ТУВ – 50/50), и немного сдвинуты в противоположном направлении при выборе опциона (4-я строка ТУВ).Таблица 2. ТУВ для узла акции.№РешениеРТСВероятность цены акции, %А5 = 5 руб.А5 = 20 руб.1d1140020802d1130050503d2140030704d213006040Завершающий этап – заполнение таблицы случайных значений полезности (Табл. 3). В ней будет всего четыре возможных значения результата инвестирования. Здесь отметим для себя, что в случае покупки опциона (d2) и курса Аа в конце месяца 5 руб. инвестор не получает ничего, но при курсе 20 руб. он получит 250 тыс. руб.Таблица 3. Состояния узла полезности.РешениеU, руб.АСК = 5 руб.АСК = 20 руб.d150000200000d20250000После заполнения всех таблиц инициализируем диаграмму, и только после этого получаем действующую модель решений нашего инвестора (Рис. 3). В таблице узла решений видим значения ожидаемых результатов инвестирования в денежном выражении: 152 тыс. руб. для решения d1, и 145 тыс. руб. для решения d2. Попробуем и в этом примере проверить машину.  Рис. 3. Модель решений инвестора.Ожидаемое значение результата покупки акции (решение d1) с учетом заданных вероятностей и каждого значения индекса РТС составит:Е(U1) = 0,2 · 50 тыс. руб. + 0,8 · 200 тыс. руб. = 170 тыс. руб. (РТС =1400)Е(U2) = 0,5 · 50 тыс. руб. + 0,5 · 200 тыс. руб. = 125 тыс. руб. (РТС =1300)Следовательно, ожидаемый результат в случае покупки акции:Е(d1) = 0,6 · 170 тыс. руб. + 0,4 · 125 тыс. руб. = 152 тыс. руб.По такому же принципу считаем ожидаемый результат в случае покупки опциона (решение d2):Е(U3) = 0,3 · 0 + 0,7 · 250 тыс. руб. = 175 тыс. руб. (РТС =1400)Е(U4) = 0,6 · 0 + 0,4 · 250 тыс. руб. = 100 тыс. руб. (РТС =1300)Следовательно, ожидаемый результат в случае покупки опциона составит:Е(d2) = 0,6 · 175 тыс. руб. + 0,4 · 100 тыс. руб. = 145 тыс. руб.Как видим, всё совпало. Инвестору остается выбрать альтернативу с наибольшей ожидаемой полезностью, поэтому его решением должна быть покупка акции, т.к. это решение дает максимальное ожидаемое значение результата инвестирования в условиях неопределенности:Е(Решение) = max (152 тыс. руб.; 145 тыс. руб.) = 152 тыс. руб.Для того чтобы продемонстрировать правильность решения кликаем мышью в строке d1 и убеждаемся, что машина оставит именно такой результат в таблице узла Решение (см. Рис. 4). При этом в строке решения d2 будет выведен нуль.  Рис. 4. Вывод окончательного решения.Для того чтобы проверить теперь уже наши расчеты, сделаем некоторые вероятностные выводы с помощью построенной модели. Например, убедимся, что при достижении индексом РТС значения 1400 (Рис. 5) модель выдает точно такие же ожидаемые результаты, которые мы получили выше, когда проверяли результаты в отдельности для случаев выбора акции или опциона.  Рис. 5. Прямой вероятностный вывод (РТС = 1400).Далее сделаем то же самое при достижении индексом РТС значения 1300 (Рис. 6), и также сверим результат.  Рис.6. Прямой вероятностный вывод (РТС = 1300).Далее усложним вывод, и зададим состояние, при котором индекс РТС достиг значения 1400, а акция Аа достигла курса 20 руб. (Рис. 7). Значения полученных результатов для такого состояния проверяем по Таблице 3.  Рис. 7. Прямой вероятностный вывод (РТС = 1400; Аа = 20 руб.).Далее проверим, что могло бы произойти, если бы курс акции Аа не достиг значения 20 руб. (Рис. 8), и получаем подтверждение того, что в этом случае выбор опциона (d2) дал бы нулевой результат при любом значении индекса РТС.  Рис. 8. Прямой вероятностный вывод (Аа = 5 руб.).Таким образом, мы убеждаемся, что даже довольно простая диаграмма влияния позволяет проводить множество интересных вероятностных выводов на построенной модели принятия решений. Опыт показывает, что диаграммы влияния пригодны для задач моделирования реальных опционов, синтетических инструментов на базе теории паритета финансовых опционов, анализа различных арбитражных возможностей, т.е. там, где неопределенностей особенно много.В данном простом примере всю таблицу полезности мы рассчитали и заполнили вручную. Однако в программах-редакторах БСД, и в Netica в частности предусмотрено заполнении таких таблиц программным путём, если известны необходимые для этого зависимости. Такие примеры мы тоже рассмотрим. =========== Источник: habr.com =========== Похожие новости:
Машинное обучение ), #_finansy_v_it ( Финансы в IT ) |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 30-Окт 06:23
Часовой пояс: UTC + 5
