[Работа с 3D-графикой, Разработка игр] Процедурная генерация деревьев методом транспорта питательных веществ (перевод)
Автор
Сообщение
news_bot ®
Стаж: 7 лет 11 месяцев
Сообщений: 27286

Примечание: код для этой статьи выложен на мой Github [здесь].
Я провёл всё лето в восточной Пенсильвании рядом с рекой Делавер, потому что кампус MIT в начале марта закрыли и мне пришлось поехать домой. Время от времени прогуливаясь рядом с домом или работой, я заходил в леса, и однажды подметил простой принцип:
Когда любая ветвь дерева разделяется, сумма площадей поперечного сечения сохраняется.
Это наблюдение уже было сделано да Винчи. Я решил воспользоваться этим наблюдением, соединить его с транспортно-ориентированной интерпретацией естественного роста деревьев, создать простую модель и нагенерировать в ней деревьев.
В данной статье будет описана эта модель и способ её использования для генерации реалистично выглядящих деревьев с разной морфологией.
При помощи этой методики можно генерировать высококачественные меши деревьев на разных этапах роста в реальном времени и с незначительной тратой вычислительных ресурсов!
Примечание: код самой модели роста дерева можно найти в файле «tree.h». Он состоит всего примерно из 250 строк кода.
Извините, данный ресурс не поддреживается. :(
Дерево с чуть более ассиметричным разделением ветвей и зелёными листьями.
Примечание: эта работа была проделана в апреле 2020 года, но я отложил написание статьи до завершения своего дипломного проекта в сентябре.
Модель роста
Дерево растёт, передавая питательные вещества вверх по структуре ветвей через внешний слой коры. В процессе роста каждый сегмент ветвей увеличивается в обхвате. Питательные вещества, добирающиеся до конца неразделённой ветви, приводят к её росту в длину, а разделённая ветвь передаёт вещества своим дочерним ветвям пропорционально некому соотношению. Для простоты мы предположим, что ветви разделяются только двоичным образом (существуют растения и с троичным разделением).
Эта концепция показана на изображении.

Транспорт вдоль дерева на примере разделения ветви, вид сбоку. Красными стрелками показаны переданные питательные вещества, а синими — рост дерева. Неразделённые ветви будут расти в обхвате и длине, а разделённые ветви растут только в обхвате. Каждая ветвь — это (конусообразный) цилиндр, поэтому рост легко описать геометрически.
У каждой ветви есть длина и радиус. На каждом шаге времени у нас есть количество питательных веществ, попадающих в ветвь. Часть веществ потребляется и преобразуется в обхват и/или длину, а остатки передаются дочерним ветвям. Когда ветвь достигает определённой длины, она разделяется и создаёт новые дочерние ветви.
Забавный факт: так как разделённая ветвь никогда не растёт в длину, качели, которые вы повесите на ветвь дерева, больше никогда не изменят своего положения или высоты относительно земли.
Реализация
Двоичное дерево хорошо подходит для рекурсивной реализации модели роста, в которой мы обрабатываем каждую ветвь по отдельности. Для этого определим struct ветви:
struct Branch{
int ID = 0; //For Leaf Hashing
bool leaf = true; //End of branch?
Branch *A, *B, *P; //Child A, B and Parent
//Growth Parameters
float ratio, spread, splitsize;
int depth = 0;
//Constructors / Destructors
//No parent
Branch(float r, float s, float ss):
ratio {r},
spread {s},
splitsize {ss}
{};
//With parent
Branch(Branch* b, bool root):
ratio {b->ratio},
spread {b->spread},
splitsize {b->splitsize}
{
if(root) return;
depth = b->depth+1;
P = b; //Set Parent
};
~Branch(){
if(leaf) return;
delete(A);
delete(B);
}
//Size / Direction Data
glm::vec3 dir = glm::vec3(0.0, 1.0, 0.0);
float length = 0.0, radius = 0.0, area = 0.1;
//Member Functions
void grow(double _size);
void split();
//Compute Direction to Highest Local Leaf Density
glm::vec3 leafdensity(int searchdepth);
};
Каждая ветвь хранит указатели на свои родительскую и дочерние ветви. Если ветвь не имеет потомков, то флаг leaf («лист») принимает значение true. У каждой ветви также есть значение depth (глубины) на дереве, при чём основной ствол имеет depth = 0.
Также мы храним геометрическую информацию ветви, включающую в себя её длину, радиус, площадь и направление в пространстве (3D-вектор).
Кроме того, структура ветви имеет две функции-элемента, описывающие весь процесс роста: grow() и split(). Подробнее они будут описаны ниже.
Примечание: деструктор ветви также уничтожит все дочерние дочерние ветви, а конструктором дочерних ветвей является только метод split().
Рост
Метод grow очень прост в реализации. В ветвь подаётся фиксированное количество питательных веществ (feed), передаваемое функции роста. Размерность этой величины можно интерпретировать как объём роста.
void Branch::grow(double feed){
radius = sqrt(area/PI); //Current Radius
//...
Если ветвь не имеет потомков, мы выращиваем её длину пропорционально кубическому корню от объёма питания. Объём питания уменьшается на потреблённую величину, а площадь вырастает на остаток. В конце мы проверяем, достаточно ли ветвь длинна для разделения, и если это так, то разделяем её и выполняем возврат:
//...
if(leaf){
length += cbrt(feed); //Grow in Length
feed -= cbrt(feed) * area; //Reduce Feed
area += feed/length; //Grow In Area
//Split Condition
if(length > splitsize * exp(-splitdecay * depth))
split(); //Split Behavior
return;
}
//...
Примечание: условие разделения проверяет, превышает ли длина пороговое значение splitsize. В этой модели пороговое значение уменьшается с увеличением глубины ветви на дереве. Выбор условия разделения полностью произволен и не основан ни на каких природных наблюдениях.
Если ветвь не является листом, то мы выращиваем её только в обхвате и передаём часть питания её потомкам.
Обратите внимание, что если ветвь оставит все питательные вещества себе, то она будет расти в обхвате, а её потомки не будут расти вообще. И наоборот — если ветвь передаст все питательные вещества потомкам, то потомки вырастут больше, чем родительская ветвь.
Следовательно, коэффициент передачи питания также определяет, будет ли сохраняться площадь поперечного сечения в конкретной развилке дерева. То есть мы можем использвать коэффициент передачи в качестве степени свободы для удовлетворения этому требованию наподобие управления с обратной связью.
Коэффициент передачи X вычисляется из площадей A всех ветвей в точке разделения (потомки A, B и родитель P):
$$display$$\begin{equation*} X = 1 - \frac{A_A + A_B}{A_A + A_B + A_P} \end{equation*}$$display$$
Он является соотношением суммы площадей дочерних ветвей и общей площади всех трёх ветвей, соединённых в точке разделения. Если площади потомков больше, чем у родителя, то мы передаём в них меньше половины питания (предел X = 0), и родительская ветвь растёт быстрее. Аналогично, если площадь родительской ветви больше суммы площадей потомков, то передаём им больше половины питания, и потомки растут быстрее (предел X = 1). Следовательно, при использовании такого определения коэффициента передачи он будет стремиться к значению, близкому к X = 0.5, что подразумевает сохранение площади поперечного сечения.
Примечание: X не будет стремиться ровно к 0.5, потому что скорость роста площади зависит от длины ветви. Для родительской ветви с потомками одинаковой длины X -> 0.5. Однако не все деревья строго следуют этому правилу ветвления (см. пример баобаба).
Затем мы соответствующим образом выращиваем ветвь:
//...
//Feedback Control for Area Conservation
double pass = (A->area+B->area)/(A->area+B->area+area);
area += pass * feed / length; //Grow in Girth
feed *= ( 1.0 - pass ); //Reduce Feed
//...
Вид деревьев зависит от параметра, определяющего асимметрию его роста (ratio). Мы передаём питательные вещества дочерним ветвям соответственно этому коэффициенту:
//...
if(feed < 1E-5) return; //Prevent Over-Branching
A->grow(feed*ratio); //Grow Children
B->grow(feed*(1.0-ratio));
}
И таким образом, наша модель роста дерева полностью описана.
Разделение
Метод split отвечает за конструирование дочерних ветвей (A и B), а также за прикрепление их соответствующим образом. Также мы используем структуру двоичного дерева для упрощения привязки каждой новой ветви к уникальному ID:
void Branch::split(){
leaf = false;
//Add Child Branches
A = new Branch(this, false);
B = new Branch(this, false);
//Every Leaf ID is Unique (because binary!)
A->ID = 2 * ID + 0;
B->ID = 2 * ID + 1;
//...
Далее каждой дочерней ветви нужно задать направление роста вперёд. Деревья естественным образом разветвляются, чтобы увеличить площадь поверхности и уменьшить самозатенение. Это биологически встроено в генетику дерева, но мы можем аппроксимировать это поведение, позволив потомкам расти перпендикулярно плоскости, образованной вектором родительской ветви и вектором, указывающим в направлении позиции с наибольшей плотностью листьев:
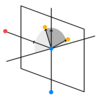
Концептуальное представление направления роста ветви. Синими точками показаны начальная и конечная точки родительской ветви, а красной — расположение наибольшей плотности листьев. Оранжевыми точками показано направление дочерних ветвей, создаваемое из направления родителя и нормали к плоскости в соответствии с коэффициентом разделения.
//...
/*
Ideal Growth Direction:
Perpendicular to direction with highest leaf density!
*/
//Direction of Highest Density
glm::vec3 D = leafdensity(localdepth);
//Normal Vector to Plane
glm::vec3 N = glm::normalize(glm::cross(dir, D));
//Reflection
glm::vec3 M = -1.0f*N;
float flip = (rand()%2)?1.0:-1.0; //Random Direction Flip
//Mix direction according to split ratio
A->dir = glm::normalize( glm::mix(flip*spread*N, dir, ratio) );
B->dir = glm::normalize( glm::mix(flip*spread*M, dir, 1.0-ratio) );
}
Затем направление дочерней ветви смешивается с направлением родительской ветви в соответствии с коэффициентом разделения, поэтому более тяжёлые ветви склонны продолжаться прямо, а лёгкие — более перпендикулярно к родителю.
Примечание: случайным образом ветвь A выбирается как тяжёлая или лёгкая. Кроме того, больше веса перпендикулярному или прямому росту может добавить параметр spread.
Локальная плотность листьев вычисляется при помощи простого алгоритма рекурсивного поиска по дереву. Мы поднимаемся по дереву на определённую глубину, а затем повторно спускаемся, чтобы вычислить среднюю позицию листьев и лямбда-функцию из геометрической информации.
glm::vec3 Branch::leafdensity(int searchdepth){
//Random Vector! (for noise)
glm::vec3 r = glm::vec3(rand()%100,rand()%100,rand()%100)/glm::vec3(100)-glm::vec3(0.5);
//Random vector for trunk
if(depth == 0)
return r;
Branch* C = this; //Ancestor node
glm::vec3 rel = glm::vec3(0); //Relative position to start node
while(C->depth > 0 && searchdepth-- >= 0){ //Ascend tree
rel += C->length*C->dir; //Add relative position
C = C->P; //Move to parent
}
//Compute Average Leaf Position of all Children (recursive)
std::function<glm::vec3(Branch*)> leafaverage = [&](Branch* b)->glm::vec3{
if(b->leaf) return b->length*b->dir;
return b->length*b->dir + ratio*leafaverage(b->A) + (1.0f-ratio)*leafaverage(b->B);
};
//Average relative to ancestor, shifted by rel ( + Noise )
return directedness*glm::normalize(leafaverage(C) - rel) + (1.0f-directedness)*r;
}
К направлению также примешивается вектор случайного шума. Соотношение между шумом и направленным ростом можно контролировать параметром directedness.
Визуализация
Примечание: эта модель роста деревьев визуализирована при помощи TinyEngine.
Структура данных двоичного дерева хорошо подходит для рекурсивного создания мешей. Каждая ветвь преобразуется в цилиндр с длиной, радиусом и конусностью. Начальная точка ветви задаётся конечной точкой её родителя, а её направление задаётся в функции split. Начальной точкой корня является просто точка начала координат.
// Model Constructing Function for Tree
std::function<void(Model*)> _construct = [&](Model* h){
//Basically Add Lines for the Tree!
std::function<void(Branch*, glm::vec3)> addBranch = [&](Branch* b, glm::vec3 p){
glm::vec3 start = p;
glm::vec3 end = p + glm::vec3(b->length*treescale[0])*b->dir;
//Get Some Normal Vector
glm::vec3 x = glm::normalize(b->dir + glm::vec3(1.0, 1.0, 1.0));
glm::vec4 n = glm::vec4(glm::normalize(glm::cross(b->dir, x)), 1.0);
//Add the Correct Number of Indices
glm::mat4 r = glm::rotate(glm::mat4(1.0), PI/ringsize, b->dir);
//Index Buffer
int _b = h->positions.size()/3;
//GL TRIANGLES
for(int i = 0; i < ringsize; i++){
//Bottom Triangle
h->indices.push_back(_b+i*2+0);
h->indices.push_back(_b+(i*2+2)%(2*ringsize));
h->indices.push_back(_b+i*2+1);
//Upper Triangle
h->indices.push_back(_b+(i*2+2)%(2*ringsize));
h->indices.push_back(_b+(i*2+3)%(2*ringsize));
h->indices.push_back(_b+i*2+1);
}
for(int i = 0; i < ringsize; i++){
h->positions.push_back(start.x + b->radius*treescale[1]*n.x);
h->positions.push_back(start.y + b->radius*treescale[1]*n.y);
h->positions.push_back(start.z + b->radius*treescale[1]*n.z);
h->normals.push_back(n.x);
h->normals.push_back(n.y);
h->normals.push_back(n.z);
n = r*n;
h->positions.push_back(end.x + taper*b->radius*treescale[1]*n.x);
h->positions.push_back(end.y + taper*b->radius*treescale[1]*n.y);
h->positions.push_back(end.z + taper*b->radius*treescale[1]*n.z);
h->normals.push_back(n.x);
h->normals.push_back(n.y);
h->normals.push_back(n.z);
n = r*n;
}
//No children
if(b->leaf) return;
addBranch(b->A, end);
addBranch(b->B, end);
};
//Recursively add Branches (at origin!)
addBranch(root, glm::vec3(0.0));
};
Модель роста обёрнута в небольшую программу, визуализирующую дерево в цвете и с расчётом теней. Небольшой интерфейс позволяет напрямую управлять параметрами роста, визуализацией и повторным выращиванием дерева.
Извините, данный ресурс не поддреживается. :(
Пример GUI процедурных деревьев для базового случая.
При помощи похожей рекурсии к деревьям для красоты были добавлены листья. Облако частиц создаётся в конечной точке всех ветвей, являющихся ветвью листьев (ниже определённой глубины). Листья используют уникальный ID каждой ветви для хэширования облака точек, чтобы визуализация при каждом шаге времени была стабильной.
Результаты
Чтобы вырастить дерево, мы просто создаём в конструкторе ветвь под названием root и продолжаем подавать по нему питательные вещества, чтобы оно росло:
int main( int argc, char* args[] ) {
//...
Branch* root;
root = new Branch({0.6, 0.45, 2.5}); //Create Root
//...
while(true){ //Not the actual game loop...
if(!paused)
root->grow(growthrate);
}
//...
return 0;
}
Эта модель роста с базовым набором параметров создаёт очень реалистичные деревья! Небольшая выборка деревьев одного «вида» показана ниже:
Извините, данный ресурс не поддреживается. :(
Выращивание процедурного дерева с базовым набором параметров при помощи моей модели. Именно это вы увидите, если скомпилируете и запустите программу.
Описанные выше параметры позволяют нам изменять морфологию дерева и генерировать разные виды. Можно настраивать коэффициент разделения, чтобы получать более асимметрично растущие деревья, например, напоминающие вечнозелёные деревья:
Извините, данный ресурс не поддреживается. :(
Рост деревьев вечнозелёного типа можно реализовать, выбрав для дочерних ветвей очень асимметричный коэффициент разделения. Стоит заметить, что здесь я использовал одинаковый спрайт листьев, но теоретически вы можете выбрать любой.
Также мы можем изменять тенденцию к прямому или перпендикулярному росту ветвей и силу, с которой они будут избегать областей с высокой плотностью листьев. Это приводит с созданию деревьев, очень напоминающих бонсай (и красиво выглядящих!):
Извините, данный ресурс не поддреживается. :(
Благодаря тому, что ветви сильнее избегают областей с высокой плотностью листьев, а также увеличению перпендикулярности дочерних ветвей дерево становится более неровным с более высокими углами. Присутствуют незначительные графические артефакты из-за того, что дерево сильно отклоняется от нормали к земле.
Таким образом, система способна воссоздавать широкий диапазон структур ветвей с двоичным разделением.
Следовательно, генерация деревьев, напоминающих конкретные виды — всего лишь вопрос косметических украшений и параметров, например, выбора спрайтов и цветов для облаков частиц листьев и подбора подходящего набора параметров роста.
Каждое сгенерированное дерево содержит элементы случайности (особенно в моменты ветвления), то есть деревья с одинаковым набором параметров будут похожими, но уникальными!
Дальнейшие размышления
Этот способ позволяет генерировать высококачественные меши процедурных деревьев на различных стадиях роста и с разными морфологиями при очень незначительном объёме кода и трате ресурсов.
Ещё одно ключевое преимущество этой системы — полная информация о структуре дерева. Структура не «запечена» в модель, а значит, геометрическую информацию можно использовать в контексте игры для таких механик, как рост фруктов, взбирание, разрушение и т.п.
Ограничение сохранения площади поперечного сечения наложено здесь в качестве граничного условия, однако оно не возникает естественным образом из более базового набора допущений о транспортировке веществ. Я надеялся, что смогу сделать так, чтобы оно основывалось на ограничении транспортировки веществ, но мне не удалось выразить это адекватно.
Кроме того, в публикациях утверждается, что сохранение площади поперечного сечения связано со структурными свойствами дерева и его устойчивостью, а не строго со свойствами транспортировки.
Модель можно усовершенствовать, дополнив разными видами ветвей, порождающими другие типы ветвей (аналогично L-системе) и созданием изменяющихся наборов параметров.
Также можно тщательнее продумать влияние наличия листьев на рост структуры ветви (обратная транспортировка питательных веществ). Для украшения модели можно добавить каждой ветви параметр возраста, что также позволит листьям время от времени «расцветать».
Улучшенная модель точного воссоздания процесса роста в ветви может ещё больше повысить реализм, однако, вероятно, будет иметь ничтожный эффект с точки зрения внешнего вида.
===========
Источник:
habr.com
===========
===========
Автор оригинала: Nicholas McDonald
===========Похожие новости:
- [C++, Разработка игр, Звук] Как не надо разрабатывать звуковые движки
- [CSS, Разработка игр, HTML] Как я IF на Twine писал
- [Работа с 3D-графикой, Интернет-маркетинг, Повышение конверсии] Еще несколько слов о 3D-обзорах: технические данные от создателей
- [Разработка игр, Разработка под Android, Unity] Разработка инди-киберпанка
- [Разработка игр, Дизайн игр, Godot] Механики ловушек и интерактивных объектов в Godot Engine. Часть 2
- [Разработка игр, Unity] Что такое Unity Asset Store и как на нем зарабатывать?
- [Программирование, C++, Работа с 3D-графикой, Разработка игр, CGI (графика)] Vulkan. Руководство разработчика
- [Разработка игр, Godot] Модули и расширения для Godot 3, ссылки и краткий обзор существующих
- [Разработка игр, Прототипирование, Дизайн игр, Godot] Микрокосм, демоверсия
- [Работа с 3D-графикой, Управление разработкой, Фриланс, Управление персоналом, Дизайн] История о том, как я не нашла инженера
Теги для поиска: #_rabota_s_3dgrafikoj (Работа с 3D-графикой), #_razrabotka_igr (Разработка игр), #_protsedurnaja_generatsija (процедурная генерация), #_protsedurnaja_generatsija_meshej (процедурная генерация мешей), #_biologija (биология), #_modelirovanie_derevev (моделирование деревьев), #_model_rosta_derevev (модель роста деревьев), #_rabota_s_3dgrafikoj (
Работа с 3D-графикой
), #_razrabotka_igr (
Разработка игр
)
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 14-Янв 18:35
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 11 месяцев |
|
 Примечание: код для этой статьи выложен на мой Github [здесь].
Я провёл всё лето в восточной Пенсильвании рядом с рекой Делавер, потому что кампус MIT в начале марта закрыли и мне пришлось поехать домой. Время от времени прогуливаясь рядом с домом или работой, я заходил в леса, и однажды подметил простой принцип: Когда любая ветвь дерева разделяется, сумма площадей поперечного сечения сохраняется. Это наблюдение уже было сделано да Винчи. Я решил воспользоваться этим наблюдением, соединить его с транспортно-ориентированной интерпретацией естественного роста деревьев, создать простую модель и нагенерировать в ней деревьев. В данной статье будет описана эта модель и способ её использования для генерации реалистично выглядящих деревьев с разной морфологией. При помощи этой методики можно генерировать высококачественные меши деревьев на разных этапах роста в реальном времени и с незначительной тратой вычислительных ресурсов! Примечание: код самой модели роста дерева можно найти в файле «tree.h». Он состоит всего примерно из 250 строк кода.
Извините, данный ресурс не поддреживается. :( Дерево с чуть более ассиметричным разделением ветвей и зелёными листьями. Примечание: эта работа была проделана в апреле 2020 года, но я отложил написание статьи до завершения своего дипломного проекта в сентябре.
Модель роста Дерево растёт, передавая питательные вещества вверх по структуре ветвей через внешний слой коры. В процессе роста каждый сегмент ветвей увеличивается в обхвате. Питательные вещества, добирающиеся до конца неразделённой ветви, приводят к её росту в длину, а разделённая ветвь передаёт вещества своим дочерним ветвям пропорционально некому соотношению. Для простоты мы предположим, что ветви разделяются только двоичным образом (существуют растения и с троичным разделением). Эта концепция показана на изображении.  Транспорт вдоль дерева на примере разделения ветви, вид сбоку. Красными стрелками показаны переданные питательные вещества, а синими — рост дерева. Неразделённые ветви будут расти в обхвате и длине, а разделённые ветви растут только в обхвате. Каждая ветвь — это (конусообразный) цилиндр, поэтому рост легко описать геометрически. У каждой ветви есть длина и радиус. На каждом шаге времени у нас есть количество питательных веществ, попадающих в ветвь. Часть веществ потребляется и преобразуется в обхват и/или длину, а остатки передаются дочерним ветвям. Когда ветвь достигает определённой длины, она разделяется и создаёт новые дочерние ветви. Забавный факт: так как разделённая ветвь никогда не растёт в длину, качели, которые вы повесите на ветвь дерева, больше никогда не изменят своего положения или высоты относительно земли. Реализация Двоичное дерево хорошо подходит для рекурсивной реализации модели роста, в которой мы обрабатываем каждую ветвь по отдельности. Для этого определим struct ветви: struct Branch{
int ID = 0; //For Leaf Hashing bool leaf = true; //End of branch? Branch *A, *B, *P; //Child A, B and Parent //Growth Parameters float ratio, spread, splitsize; int depth = 0; //Constructors / Destructors //No parent Branch(float r, float s, float ss): ratio {r}, spread {s}, splitsize {ss} {}; //With parent Branch(Branch* b, bool root): ratio {b->ratio}, spread {b->spread}, splitsize {b->splitsize} { if(root) return; depth = b->depth+1; P = b; //Set Parent }; ~Branch(){ if(leaf) return; delete(A); delete(B); } //Size / Direction Data glm::vec3 dir = glm::vec3(0.0, 1.0, 0.0); float length = 0.0, radius = 0.0, area = 0.1; //Member Functions void grow(double _size); void split(); //Compute Direction to Highest Local Leaf Density glm::vec3 leafdensity(int searchdepth); }; Каждая ветвь хранит указатели на свои родительскую и дочерние ветви. Если ветвь не имеет потомков, то флаг leaf («лист») принимает значение true. У каждой ветви также есть значение depth (глубины) на дереве, при чём основной ствол имеет depth = 0. Также мы храним геометрическую информацию ветви, включающую в себя её длину, радиус, площадь и направление в пространстве (3D-вектор). Кроме того, структура ветви имеет две функции-элемента, описывающие весь процесс роста: grow() и split(). Подробнее они будут описаны ниже. Примечание: деструктор ветви также уничтожит все дочерние дочерние ветви, а конструктором дочерних ветвей является только метод split().
Рост Метод grow очень прост в реализации. В ветвь подаётся фиксированное количество питательных веществ (feed), передаваемое функции роста. Размерность этой величины можно интерпретировать как объём роста. void Branch::grow(double feed){
radius = sqrt(area/PI); //Current Radius //... Если ветвь не имеет потомков, мы выращиваем её длину пропорционально кубическому корню от объёма питания. Объём питания уменьшается на потреблённую величину, а площадь вырастает на остаток. В конце мы проверяем, достаточно ли ветвь длинна для разделения, и если это так, то разделяем её и выполняем возврат: //...
if(leaf){ length += cbrt(feed); //Grow in Length feed -= cbrt(feed) * area; //Reduce Feed area += feed/length; //Grow In Area //Split Condition if(length > splitsize * exp(-splitdecay * depth)) split(); //Split Behavior return; } //... Примечание: условие разделения проверяет, превышает ли длина пороговое значение splitsize. В этой модели пороговое значение уменьшается с увеличением глубины ветви на дереве. Выбор условия разделения полностью произволен и не основан ни на каких природных наблюдениях.
Если ветвь не является листом, то мы выращиваем её только в обхвате и передаём часть питания её потомкам. Обратите внимание, что если ветвь оставит все питательные вещества себе, то она будет расти в обхвате, а её потомки не будут расти вообще. И наоборот — если ветвь передаст все питательные вещества потомкам, то потомки вырастут больше, чем родительская ветвь. Следовательно, коэффициент передачи питания также определяет, будет ли сохраняться площадь поперечного сечения в конкретной развилке дерева. То есть мы можем использвать коэффициент передачи в качестве степени свободы для удовлетворения этому требованию наподобие управления с обратной связью. Коэффициент передачи X вычисляется из площадей A всех ветвей в точке разделения (потомки A, B и родитель P): $$display$$\begin{equation*} X = 1 - \frac{A_A + A_B}{A_A + A_B + A_P} \end{equation*}$$display$$ Он является соотношением суммы площадей дочерних ветвей и общей площади всех трёх ветвей, соединённых в точке разделения. Если площади потомков больше, чем у родителя, то мы передаём в них меньше половины питания (предел X = 0), и родительская ветвь растёт быстрее. Аналогично, если площадь родительской ветви больше суммы площадей потомков, то передаём им больше половины питания, и потомки растут быстрее (предел X = 1). Следовательно, при использовании такого определения коэффициента передачи он будет стремиться к значению, близкому к X = 0.5, что подразумевает сохранение площади поперечного сечения. Примечание: X не будет стремиться ровно к 0.5, потому что скорость роста площади зависит от длины ветви. Для родительской ветви с потомками одинаковой длины X -> 0.5. Однако не все деревья строго следуют этому правилу ветвления (см. пример баобаба).
Затем мы соответствующим образом выращиваем ветвь: //...
//Feedback Control for Area Conservation double pass = (A->area+B->area)/(A->area+B->area+area); area += pass * feed / length; //Grow in Girth feed *= ( 1.0 - pass ); //Reduce Feed //... Вид деревьев зависит от параметра, определяющего асимметрию его роста (ratio). Мы передаём питательные вещества дочерним ветвям соответственно этому коэффициенту: //...
if(feed < 1E-5) return; //Prevent Over-Branching A->grow(feed*ratio); //Grow Children B->grow(feed*(1.0-ratio)); } И таким образом, наша модель роста дерева полностью описана. Разделение Метод split отвечает за конструирование дочерних ветвей (A и B), а также за прикрепление их соответствующим образом. Также мы используем структуру двоичного дерева для упрощения привязки каждой новой ветви к уникальному ID: void Branch::split(){
leaf = false; //Add Child Branches A = new Branch(this, false); B = new Branch(this, false); //Every Leaf ID is Unique (because binary!) A->ID = 2 * ID + 0; B->ID = 2 * ID + 1; //... Далее каждой дочерней ветви нужно задать направление роста вперёд. Деревья естественным образом разветвляются, чтобы увеличить площадь поверхности и уменьшить самозатенение. Это биологически встроено в генетику дерева, но мы можем аппроксимировать это поведение, позволив потомкам расти перпендикулярно плоскости, образованной вектором родительской ветви и вектором, указывающим в направлении позиции с наибольшей плотностью листьев:  Концептуальное представление направления роста ветви. Синими точками показаны начальная и конечная точки родительской ветви, а красной — расположение наибольшей плотности листьев. Оранжевыми точками показано направление дочерних ветвей, создаваемое из направления родителя и нормали к плоскости в соответствии с коэффициентом разделения. //...
/* Ideal Growth Direction: Perpendicular to direction with highest leaf density! */ //Direction of Highest Density glm::vec3 D = leafdensity(localdepth); //Normal Vector to Plane glm::vec3 N = glm::normalize(glm::cross(dir, D)); //Reflection glm::vec3 M = -1.0f*N; float flip = (rand()%2)?1.0:-1.0; //Random Direction Flip //Mix direction according to split ratio A->dir = glm::normalize( glm::mix(flip*spread*N, dir, ratio) ); B->dir = glm::normalize( glm::mix(flip*spread*M, dir, 1.0-ratio) ); } Затем направление дочерней ветви смешивается с направлением родительской ветви в соответствии с коэффициентом разделения, поэтому более тяжёлые ветви склонны продолжаться прямо, а лёгкие — более перпендикулярно к родителю. Примечание: случайным образом ветвь A выбирается как тяжёлая или лёгкая. Кроме того, больше веса перпендикулярному или прямому росту может добавить параметр spread.
Локальная плотность листьев вычисляется при помощи простого алгоритма рекурсивного поиска по дереву. Мы поднимаемся по дереву на определённую глубину, а затем повторно спускаемся, чтобы вычислить среднюю позицию листьев и лямбда-функцию из геометрической информации. glm::vec3 Branch::leafdensity(int searchdepth){
//Random Vector! (for noise) glm::vec3 r = glm::vec3(rand()%100,rand()%100,rand()%100)/glm::vec3(100)-glm::vec3(0.5); //Random vector for trunk if(depth == 0) return r; Branch* C = this; //Ancestor node glm::vec3 rel = glm::vec3(0); //Relative position to start node while(C->depth > 0 && searchdepth-- >= 0){ //Ascend tree rel += C->length*C->dir; //Add relative position C = C->P; //Move to parent } //Compute Average Leaf Position of all Children (recursive) std::function<glm::vec3(Branch*)> leafaverage = [&](Branch* b)->glm::vec3{ if(b->leaf) return b->length*b->dir; return b->length*b->dir + ratio*leafaverage(b->A) + (1.0f-ratio)*leafaverage(b->B); }; //Average relative to ancestor, shifted by rel ( + Noise ) return directedness*glm::normalize(leafaverage(C) - rel) + (1.0f-directedness)*r; } К направлению также примешивается вектор случайного шума. Соотношение между шумом и направленным ростом можно контролировать параметром directedness. Визуализация Примечание: эта модель роста деревьев визуализирована при помощи TinyEngine.
Структура данных двоичного дерева хорошо подходит для рекурсивного создания мешей. Каждая ветвь преобразуется в цилиндр с длиной, радиусом и конусностью. Начальная точка ветви задаётся конечной точкой её родителя, а её направление задаётся в функции split. Начальной точкой корня является просто точка начала координат. // Model Constructing Function for Tree
std::function<void(Model*)> _construct = [&](Model* h){ //Basically Add Lines for the Tree! std::function<void(Branch*, glm::vec3)> addBranch = [&](Branch* b, glm::vec3 p){ glm::vec3 start = p; glm::vec3 end = p + glm::vec3(b->length*treescale[0])*b->dir; //Get Some Normal Vector glm::vec3 x = glm::normalize(b->dir + glm::vec3(1.0, 1.0, 1.0)); glm::vec4 n = glm::vec4(glm::normalize(glm::cross(b->dir, x)), 1.0); //Add the Correct Number of Indices glm::mat4 r = glm::rotate(glm::mat4(1.0), PI/ringsize, b->dir); //Index Buffer int _b = h->positions.size()/3; //GL TRIANGLES for(int i = 0; i < ringsize; i++){ //Bottom Triangle h->indices.push_back(_b+i*2+0); h->indices.push_back(_b+(i*2+2)%(2*ringsize)); h->indices.push_back(_b+i*2+1); //Upper Triangle h->indices.push_back(_b+(i*2+2)%(2*ringsize)); h->indices.push_back(_b+(i*2+3)%(2*ringsize)); h->indices.push_back(_b+i*2+1); } for(int i = 0; i < ringsize; i++){ h->positions.push_back(start.x + b->radius*treescale[1]*n.x); h->positions.push_back(start.y + b->radius*treescale[1]*n.y); h->positions.push_back(start.z + b->radius*treescale[1]*n.z); h->normals.push_back(n.x); h->normals.push_back(n.y); h->normals.push_back(n.z); n = r*n; h->positions.push_back(end.x + taper*b->radius*treescale[1]*n.x); h->positions.push_back(end.y + taper*b->radius*treescale[1]*n.y); h->positions.push_back(end.z + taper*b->radius*treescale[1]*n.z); h->normals.push_back(n.x); h->normals.push_back(n.y); h->normals.push_back(n.z); n = r*n; } //No children if(b->leaf) return; addBranch(b->A, end); addBranch(b->B, end); }; //Recursively add Branches (at origin!) addBranch(root, glm::vec3(0.0)); }; Модель роста обёрнута в небольшую программу, визуализирующую дерево в цвете и с расчётом теней. Небольшой интерфейс позволяет напрямую управлять параметрами роста, визуализацией и повторным выращиванием дерева. Извините, данный ресурс не поддреживается. :( Пример GUI процедурных деревьев для базового случая. При помощи похожей рекурсии к деревьям для красоты были добавлены листья. Облако частиц создаётся в конечной точке всех ветвей, являющихся ветвью листьев (ниже определённой глубины). Листья используют уникальный ID каждой ветви для хэширования облака точек, чтобы визуализация при каждом шаге времени была стабильной. Результаты Чтобы вырастить дерево, мы просто создаём в конструкторе ветвь под названием root и продолжаем подавать по нему питательные вещества, чтобы оно росло: int main( int argc, char* args[] ) {
//... Branch* root; root = new Branch({0.6, 0.45, 2.5}); //Create Root //... while(true){ //Not the actual game loop... if(!paused) root->grow(growthrate); } //... return 0; } Эта модель роста с базовым набором параметров создаёт очень реалистичные деревья! Небольшая выборка деревьев одного «вида» показана ниже: Извините, данный ресурс не поддреживается. :( Выращивание процедурного дерева с базовым набором параметров при помощи моей модели. Именно это вы увидите, если скомпилируете и запустите программу. Описанные выше параметры позволяют нам изменять морфологию дерева и генерировать разные виды. Можно настраивать коэффициент разделения, чтобы получать более асимметрично растущие деревья, например, напоминающие вечнозелёные деревья: Извините, данный ресурс не поддреживается. :( Рост деревьев вечнозелёного типа можно реализовать, выбрав для дочерних ветвей очень асимметричный коэффициент разделения. Стоит заметить, что здесь я использовал одинаковый спрайт листьев, но теоретически вы можете выбрать любой. Также мы можем изменять тенденцию к прямому или перпендикулярному росту ветвей и силу, с которой они будут избегать областей с высокой плотностью листьев. Это приводит с созданию деревьев, очень напоминающих бонсай (и красиво выглядящих!): Извините, данный ресурс не поддреживается. :( Благодаря тому, что ветви сильнее избегают областей с высокой плотностью листьев, а также увеличению перпендикулярности дочерних ветвей дерево становится более неровным с более высокими углами. Присутствуют незначительные графические артефакты из-за того, что дерево сильно отклоняется от нормали к земле. Таким образом, система способна воссоздавать широкий диапазон структур ветвей с двоичным разделением. Следовательно, генерация деревьев, напоминающих конкретные виды — всего лишь вопрос косметических украшений и параметров, например, выбора спрайтов и цветов для облаков частиц листьев и подбора подходящего набора параметров роста. Каждое сгенерированное дерево содержит элементы случайности (особенно в моменты ветвления), то есть деревья с одинаковым набором параметров будут похожими, но уникальными! Дальнейшие размышления Этот способ позволяет генерировать высококачественные меши процедурных деревьев на различных стадиях роста и с разными морфологиями при очень незначительном объёме кода и трате ресурсов. Ещё одно ключевое преимущество этой системы — полная информация о структуре дерева. Структура не «запечена» в модель, а значит, геометрическую информацию можно использовать в контексте игры для таких механик, как рост фруктов, взбирание, разрушение и т.п. Ограничение сохранения площади поперечного сечения наложено здесь в качестве граничного условия, однако оно не возникает естественным образом из более базового набора допущений о транспортировке веществ. Я надеялся, что смогу сделать так, чтобы оно основывалось на ограничении транспортировки веществ, но мне не удалось выразить это адекватно. Кроме того, в публикациях утверждается, что сохранение площади поперечного сечения связано со структурными свойствами дерева и его устойчивостью, а не строго со свойствами транспортировки. Модель можно усовершенствовать, дополнив разными видами ветвей, порождающими другие типы ветвей (аналогично L-системе) и созданием изменяющихся наборов параметров. Также можно тщательнее продумать влияние наличия листьев на рост структуры ветви (обратная транспортировка питательных веществ). Для украшения модели можно добавить каждой ветви параметр возраста, что также позволит листьям время от времени «расцветать». Улучшенная модель точного воссоздания процесса роста в ветви может ещё больше повысить реализм, однако, вероятно, будет иметь ничтожный эффект с точки зрения внешнего вида. =========== Источник: habr.com =========== =========== Автор оригинала: Nicholas McDonald ===========Похожие новости:
Работа с 3D-графикой ), #_razrabotka_igr ( Разработка игр ) |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 14-Янв 18:35
Часовой пояс: UTC + 5
