[Программирование, Математика, Matlab] Реализация моделей динамических систем средствами контроллера
Автор
Сообщение
news_bot ®
Стаж: 7 лет 10 месяцев
Сообщений: 27286
За основу задания динамических свойств систем может быть принята любая из форм представления операторов: дифференциальные уравнения (ДУ), передаточные функции (ПФ), временные характеристики (ВХ) или частотные характеристики (ЧХ), однако для конкретных задач целесообразно выбирать наиболее рациональную форму [1].
Возможные преобразования форм представления моделей вход-выход показаны на Рисунок 1. Сплошные линии орграфа показывают однозначные преобразования, штриховые - неоднозначные преобразования экспериментальных данных. Результаты последних преобразований зависят от выбора структуры оператора и алгоритма обработки данных. 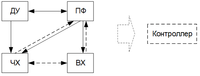
Рисунок 1. Орграф взаимосвязи форм представления моделей. Модели могут описывать поведение регуляторов систем управления [4], наблюдателей [3], корректирующих звеньев, фильтров [5], и др. динамических систем. В этой работе рассматриваются MATLAB преобразования форм представления моделей и реализация моделей средствами контроллеров. Дискретная модель объекта
Для сравнения результатов преобразования моделей будем использовать одну и ту же систему - объект третьего порядка, дискретная модель которого в форме пространства состояний имеет следующие коэффициенты. 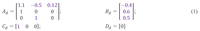
Дискретная модель в форме пространства состояний представляется разностными уравнениями первого порядка 
Связь переменных уравнений (2) показана на блок схеме Рисунок 2, где X – переменные состояния; 1/z – задержка на один такт. 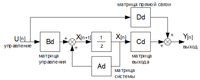
Рисунок 2. Структура дискретной модели объекта в форме пространства состояний. Система разностных уравнений
Раскроем уравнения (2) подстановкой в уравнения матриц (1) объекта:

По разностным уравнениям (3) построим Simulink модель дискретного объекта с периодом дискретизации 1 с (см. Рисунок 3). 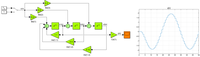
Рисунок 3. Дискретная модель объекта (1) и реакция y[n] объекта на синусоидальное u[n] воздействие. Импульсная передаточная функция
Воспользуемся преобразованием форм MATLAB для перевода дискретной модели из пространства состояний в формат импульсной передаточной функции, затем в формат непрерывной ПФ и, наконец, в формат пространства состояний непрерывной модели. Ниже показан код m-программы c промежуточными результатами, сдвинутыми вправо на 1 Tab.
Ad = [1.1 -0.5 0.12
1.0 0.0 0.0
0.0 1.0 0.0];Bd = [-0.4
0.6
0.5];Cd = [1 0 0];Dd = 0;
Wo_ss_d = ss(Ad,Bd,Cd,Dd,1); % структура дискретной модели с периодом 1 с
Wo_tf_d = tf(Wo_ss_d) % дискретная ПФ

Непрерывная передаточная функцияWo_tf_c = d2c(Wo_tf_d) % непрерывная ПФ
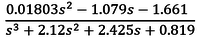
Непрерывная модель в форме пространства состояний
Wo_ss_c = ss(Wo_tf_c) % непрерывная модель в форме пространства состояний
Wo_ss_c =
A =
x1 x2 x3 (4)
x1 -2.12 -1.213 -0.819
x2 2 0 0
x3 0 0.5 0
B =
u1
x1 2
x2 0
x3 0
C =
x1 x2 x3
y1 0.009016 -0.2697 -0.8307
D =
u1
y1 0Continuous-time state-space model.ВНИМАНИЕ. Изменение шага дискретизации приводит к соответствующему изменению динамики модели. Для того, чтобы эквивалентная непрерывная модель “не отставала” и “не убегала” от дискретной модели с новым шагом дискретизации, необходимо пересчитать коэффициенты непрерывной модели.Приведенный многоступенчатый перевод дискретной модели (1, 2, 3) в непрерывную модель пространства состояний (4) можно выполнить одной командой d2c: Wo_ss_c = d2c(Wo_ss_d). В этом варианте получится набор матриц с другими коэффициентами относительно многоступенчатого варианта, но это не является ошибкой, поскольку одна и та же ПФ (с одинаковым составом нулей и полюсов) может быть представлена в форме пространства состояний разными вариантами коэффициентов матриц A, B, C, D. Нули и полюса ПФ можно вычислить командами MATLAB: zeros, poles, eig. Система дифференциальных уравнений
Матрицы (4) непрерывной модели связывают переменные состояния x(t) с входом y(t) и выходом u(t) модели следующим образом.

Раскроем систему дифференциальных уравнений (5) подстановкой коэффициентов матриц (4): 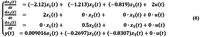
Как в случае построения дискретной Simulink модели (Рисунок 3) по разностным уравнениям (3), построим Simulink модель непрерывного объекта (см. Рисунок 4) по дифференциальным уравнениям (6). 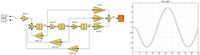
Рисунок 4. Непрерывная модель объекта (1) и реакция y(t) объекта на синусоидальное u(t) воздействие (синий график). Для сравнения, показан коричневый график y[n] дискретного объекта Рисунок 3, график y(t) сдвинут вправо на 0.5 с - половину дискреты. Перевод модели в частотную область
В MATLAB по данным модели пространства состояний или передаточным функциям можно построить соответствующие амплитудно-фазовые частотные характеристики (АФЧХ). Примеры перевода для рассматриваемого объекта показаны ниже.
bode(Wo_ss_d) % АФЧХ дискретного объекта представленного в форме пространства состояний
bode(Wo_tf_d) % АФЧХ дискретного объекта представленного в форме ПФ
bode(Wo_ss_c) % АФЧХ непрерывного объекта представленного в форме пространства состояний
bode(Wo_tf_c) % АФЧХ непрерывного объекта представленного в форме ПФ
grid % нанесение координатной сетки

Рисунок 5. Амплитудно-фазовые частотные характеристики непрерывного объекта (слева) и дискретного объекта (справа). Построение передаточной функции по частотным характеристикам
Имеется множество вариантов обратного перевода модели из частотной области. Вот один из них.
[mag,phase,freq] = bode(Wo_tf_c) % выделение амплитуды, фазы и частоты АФЧХ
complex_f = frd(mag.exp(jphase.pi/180),freq) % модель объекта в частотной области tfest(complex_f,3) % ПФ непрерывного объекта, 3 - порядок объекта 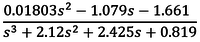
В этом примере зависимости амплитуды mag и фазы phase от частоты freq вычислены оператором bode для ПФ Wo_tf_c. Оператор frd сформировал структуру complex_f - зависимость комплексных аргументов mag.exp(jphase.pi/180) от частоты, которая использовалась оператором tfest для построения ПФ непрерывного объекта третьего порядка. Полученная ПФ точно совпадает с исходной ПФ Wo_tf_c. Как упоминалось во введении, при использовании экспериментальных зависимостей (амплитуды и фазы от частоты) мы бы получили неоднозначный вариант ПФ. Перевод модели во временную область
MATLAB предлагает множество вариантов вычисления реакции объекта на входное воздействие. Вот один из них – реакция (Рисунок 6) на единичное ступенчатое воздействие вычисляется оператором step:
% [y,t] = step(Wo_tf_c) % выделение данных реакции на единичное воздействие
step(Wo_tf_c) % построение графика реакции на единичное воздействие

Рисунок 6. Реакция модели непрерывного объекта (ПФ: Wo_tf_c) на единичное ступенчатое воздействие. Построение передаточной функции по временным характеристикам
Обратное преобразование – построение передаточной функции по временным характеристикам входа и выхода объекта выполняется командами iddata и tfest.Перевод импульсной передаточной функции в код контроллера
Модель Рисунок 3 импульсной передаточной функции (3a) дискретного объекта (1) можно представить в виде схемы показанной на Рисунок 7.
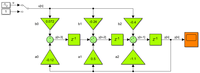
Рисунок 7. Модель импульсной передаточной функции 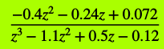
. Блок z-1 реализует задержку на 1 такт. Для рассматриваемого объекта установлен период дискретизации в 1 с. Работа схемы Рисунок 7 подобна реализации Рисунок 8, в которой блок fcn, содержащий m-функцию пользователя, выполняет совместно с z-1 блоками работу рассматриваемой импульсной ПФ. 
Рисунок 8. Simulink модель эквивалентной импульсной передаточной функции с fcn блоком, содержащим представленный m-код. Следующая программа вычисляет реакцию объекта, представленного импульсной ПФ. Полученная реакция (Рисунок 9) полностью совпадает с реакциями дискретных моделей рассматриваемого объекта и соответствует реакциям непрерывных моделей этого же объекта (Рисунок 10). b2 = -0.4; b1 = -0.24; b0 = 0.072; % коэффициенты полинома числителя ИПФ a3 = 1; a2 = -1.1; a1 = 0.5; a0 = -0.12; % коэффициенты полинома знаменателя ИПФ y = zeros(1,50); % резервирование памяти для хранения реакции
u = ones(1,50); % единичное воздействиеym1 = 0; ym2 = 0; ym3 = 0 % начальные значения for i = 1:50 y(i) = a3*ym1; (7) ym1 = b2*u(i)-a2*y(i)+ym2; ym2 = b1*u(i)-a1*y(i)+ym3; ym3 = b0*u(i)-a0*y(i);end% График реакции дискретных моделей if 1
% Построение графиков
figure (1) % активное окно графопостроителя
clf % очистка предыдущих данных
plot(y,'xb') % график y[n] m-файла
hold on
plot(out.ScopeData1.signals(3).values) % график y[n] Simulink модели, ver.1
plot(out.ScopeData1.signals(4).values) % график y[n] Simulink модели, ver.2
plot(out.ScopeData1.signals(5).values) % график y[n] Simulink модели, ver.3
plot(out.ScopeData1.signals(6).values) % график y[n] Simulink модели, ver.4
legend('m-file','Simulink v.1','Simulink v.2','Simulink v.3','Simulink v.4')
grid
xlabel('Номер отсчета')
ylabel('Амплитуда реакции'),
title('Сравнение реакций дискретных моделей')
end

Рисунок 9. 100% совпадение реакций дискретных моделей и вычислений m-программы. 
Рисунок 10. Варианты построения эквивалентных Simulink моделей рассматриваемого объекта. Порядок программирования динамических моделей контроллерами
Для построения модели динамической системы средствами контроллеров предлагается выполнить следующее.
- Средствами MATLAB преобразовать динамическую систему в форму импульсной передаточной функции для требуемого шага дискретизации (3a).
- Выделить коэффициенты полиномов числителя и знаменателя импульсной ПФ (Рисунок 7)
- Средствами контроллера реализовать последовательность вычисления импульсной ПФ (7)
Структура и порядок динамической системы могут отличаться от рассмотренного примера. Заключение
Рассмотренные варианты преобразования форм представления динамических моделей в интегрированной среде MATLAB могут быть использованы для реализации моделей средствами контроллеров путем построения кода эквивалентной импульсной передаточной функции (Рисунок 11).
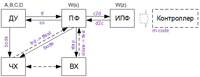
Рисунок 11. Операторы MATLAB преобразования моделей и построения эквивалентного кода для программирования контроллеров. БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- А.А.Алексеев, Д.Х.Имаев, Н.Н.Кузьмин, В.Б.Яковлев. Теория управления: Учеб./СПб.: Изд-во СПбГЭТУ “ЛЭТИ”, 1999. – 435 с.
- Help MATLAB.
- Dr. Bob Davidov. Синтез наблюдателя состояний. http://portalnp.ru/2021/01/10862
- Dr. Bob Davidov. Аналитическое конструирование линейно-квадратичного регулятора http://portalnp.ru/2021/01/10857
- Dr. Bob Davidov. Фильтр Калмана в линейно-квадратичном гауссовском управлении. http://portalnp.ru/2021/02/10877
===========
Источник:
habr.com
===========
Похожие новости:
- [Математика, Суперкомпьютеры] Как суперкомпьютеры нашли свое промышленное mojo — эволюция высокопроизводительных вычислений (перевод)
- [Программирование, C++, Qt, Visual Studio, DevOps] О поиске утечек памяти в С++/Qt приложениях
- [Open source, Программирование, C++] [sobjectizer] Можно ли написать один обработчик сразу для нескольких типов сообщений? И если нет, то как быть?
- [Программирование, .NET, Разработка под MacOS, Разработка под Windows] От WPF к Авалонии
- [Python, Программирование, Машинное обучение] Подбор гиперпараметров ML-модели с помощью HYPEROPT
- [Разработка веб-сайтов, JavaScript, Программирование, ReactJS] 5 подходов к стилизации React-компонентов на примере одного приложения
- [Информационная безопасность, PHP, Программирование] Защита от уязвимости Dependency Confusion в PHP с помощью Composer (перевод)
- [JavaScript, Программирование, Учебный процесс в IT] Мои рассуждения на тему Как учиться программировать на JavaScript
- [Математика, Машинное обучение, Будущее здесь] Ученые создали машину для изобретения математики
- [Python, Программирование] Разбираемся с not в Python (перевод)
Теги для поиска: #_programmirovanie (Программирование), #_matematika (Математика), #_matlab, #_opisanie_dinamicheskih_sistem (Описание динамических систем), #_preobrazovanie_modelej (Преобразование моделей), #_peredatochnye_funktsii (Передаточные функции), #_programmirovanie (
Программирование
), #_matematika (
Математика
), #_matlab
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 15-Дек 00:23
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 10 месяцев |
|
|
За основу задания динамических свойств систем может быть принята любая из форм представления операторов: дифференциальные уравнения (ДУ), передаточные функции (ПФ), временные характеристики (ВХ) или частотные характеристики (ЧХ), однако для конкретных задач целесообразно выбирать наиболее рациональную форму [1]. Возможные преобразования форм представления моделей вход-выход показаны на Рисунок 1. Сплошные линии орграфа показывают однозначные преобразования, штриховые - неоднозначные преобразования экспериментальных данных. Результаты последних преобразований зависят от выбора структуры оператора и алгоритма обработки данных.  Рисунок 1. Орграф взаимосвязи форм представления моделей. Модели могут описывать поведение регуляторов систем управления [4], наблюдателей [3], корректирующих звеньев, фильтров [5], и др. динамических систем. В этой работе рассматриваются MATLAB преобразования форм представления моделей и реализация моделей средствами контроллеров. Дискретная модель объекта Для сравнения результатов преобразования моделей будем использовать одну и ту же систему - объект третьего порядка, дискретная модель которого в форме пространства состояний имеет следующие коэффициенты. 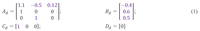 Дискретная модель в форме пространства состояний представляется разностными уравнениями первого порядка  Связь переменных уравнений (2) показана на блок схеме Рисунок 2, где X – переменные состояния; 1/z – задержка на один такт.  Рисунок 2. Структура дискретной модели объекта в форме пространства состояний. Система разностных уравнений Раскроем уравнения (2) подстановкой в уравнения матриц (1) объекта:  По разностным уравнениям (3) построим Simulink модель дискретного объекта с периодом дискретизации 1 с (см. Рисунок 3).  Рисунок 3. Дискретная модель объекта (1) и реакция y[n] объекта на синусоидальное u[n] воздействие. Импульсная передаточная функция Воспользуемся преобразованием форм MATLAB для перевода дискретной модели из пространства состояний в формат импульсной передаточной функции, затем в формат непрерывной ПФ и, наконец, в формат пространства состояний непрерывной модели. Ниже показан код m-программы c промежуточными результатами, сдвинутыми вправо на 1 Tab. Ad = [1.1 -0.5 0.12 1.0 0.0 0.0 0.0 1.0 0.0];Bd = [-0.4 0.6 0.5];Cd = [1 0 0];Dd = 0; Wo_ss_d = ss(Ad,Bd,Cd,Dd,1); % структура дискретной модели с периодом 1 с Wo_tf_d = tf(Wo_ss_d) % дискретная ПФ  Непрерывная передаточная функцияWo_tf_c = d2c(Wo_tf_d) % непрерывная ПФ 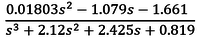 Непрерывная модель в форме пространства состояний Wo_ss_c = ss(Wo_tf_c) % непрерывная модель в форме пространства состояний Wo_ss_c = A = x1 x2 x3 (4) x1 -2.12 -1.213 -0.819 x2 2 0 0 x3 0 0.5 0 B = u1 x1 2 x2 0 x3 0 C = x1 x2 x3 y1 0.009016 -0.2697 -0.8307 D = u1 y1 0Continuous-time state-space model.ВНИМАНИЕ. Изменение шага дискретизации приводит к соответствующему изменению динамики модели. Для того, чтобы эквивалентная непрерывная модель “не отставала” и “не убегала” от дискретной модели с новым шагом дискретизации, необходимо пересчитать коэффициенты непрерывной модели.Приведенный многоступенчатый перевод дискретной модели (1, 2, 3) в непрерывную модель пространства состояний (4) можно выполнить одной командой d2c: Wo_ss_c = d2c(Wo_ss_d). В этом варианте получится набор матриц с другими коэффициентами относительно многоступенчатого варианта, но это не является ошибкой, поскольку одна и та же ПФ (с одинаковым составом нулей и полюсов) может быть представлена в форме пространства состояний разными вариантами коэффициентов матриц A, B, C, D. Нули и полюса ПФ можно вычислить командами MATLAB: zeros, poles, eig. Система дифференциальных уравнений Матрицы (4) непрерывной модели связывают переменные состояния x(t) с входом y(t) и выходом u(t) модели следующим образом.  Раскроем систему дифференциальных уравнений (5) подстановкой коэффициентов матриц (4): 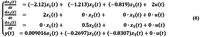 Как в случае построения дискретной Simulink модели (Рисунок 3) по разностным уравнениям (3), построим Simulink модель непрерывного объекта (см. Рисунок 4) по дифференциальным уравнениям (6).  Рисунок 4. Непрерывная модель объекта (1) и реакция y(t) объекта на синусоидальное u(t) воздействие (синий график). Для сравнения, показан коричневый график y[n] дискретного объекта Рисунок 3, график y(t) сдвинут вправо на 0.5 с - половину дискреты. Перевод модели в частотную область В MATLAB по данным модели пространства состояний или передаточным функциям можно построить соответствующие амплитудно-фазовые частотные характеристики (АФЧХ). Примеры перевода для рассматриваемого объекта показаны ниже. bode(Wo_ss_d) % АФЧХ дискретного объекта представленного в форме пространства состояний bode(Wo_tf_d) % АФЧХ дискретного объекта представленного в форме ПФ bode(Wo_ss_c) % АФЧХ непрерывного объекта представленного в форме пространства состояний bode(Wo_tf_c) % АФЧХ непрерывного объекта представленного в форме ПФ grid % нанесение координатной сетки  Рисунок 5. Амплитудно-фазовые частотные характеристики непрерывного объекта (слева) и дискретного объекта (справа). Построение передаточной функции по частотным характеристикам Имеется множество вариантов обратного перевода модели из частотной области. Вот один из них. [mag,phase,freq] = bode(Wo_tf_c) % выделение амплитуды, фазы и частоты АФЧХ complex_f = frd(mag.exp(jphase.pi/180),freq) % модель объекта в частотной области tfest(complex_f,3) % ПФ непрерывного объекта, 3 - порядок объекта 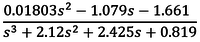 В этом примере зависимости амплитуды mag и фазы phase от частоты freq вычислены оператором bode для ПФ Wo_tf_c. Оператор frd сформировал структуру complex_f - зависимость комплексных аргументов mag.exp(jphase.pi/180) от частоты, которая использовалась оператором tfest для построения ПФ непрерывного объекта третьего порядка. Полученная ПФ точно совпадает с исходной ПФ Wo_tf_c. Как упоминалось во введении, при использовании экспериментальных зависимостей (амплитуды и фазы от частоты) мы бы получили неоднозначный вариант ПФ. Перевод модели во временную область MATLAB предлагает множество вариантов вычисления реакции объекта на входное воздействие. Вот один из них – реакция (Рисунок 6) на единичное ступенчатое воздействие вычисляется оператором step: % [y,t] = step(Wo_tf_c) % выделение данных реакции на единичное воздействие step(Wo_tf_c) % построение графика реакции на единичное воздействие  Рисунок 6. Реакция модели непрерывного объекта (ПФ: Wo_tf_c) на единичное ступенчатое воздействие. Построение передаточной функции по временным характеристикам Обратное преобразование – построение передаточной функции по временным характеристикам входа и выхода объекта выполняется командами iddata и tfest.Перевод импульсной передаточной функции в код контроллера Модель Рисунок 3 импульсной передаточной функции (3a) дискретного объекта (1) можно представить в виде схемы показанной на Рисунок 7.  Рисунок 7. Модель импульсной передаточной функции 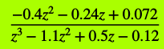 . Блок z-1 реализует задержку на 1 такт. Для рассматриваемого объекта установлен период дискретизации в 1 с. Работа схемы Рисунок 7 подобна реализации Рисунок 8, в которой блок fcn, содержащий m-функцию пользователя, выполняет совместно с z-1 блоками работу рассматриваемой импульсной ПФ.  Рисунок 8. Simulink модель эквивалентной импульсной передаточной функции с fcn блоком, содержащим представленный m-код. Следующая программа вычисляет реакцию объекта, представленного импульсной ПФ. Полученная реакция (Рисунок 9) полностью совпадает с реакциями дискретных моделей рассматриваемого объекта и соответствует реакциям непрерывных моделей этого же объекта (Рисунок 10). b2 = -0.4; b1 = -0.24; b0 = 0.072; % коэффициенты полинома числителя ИПФ a3 = 1; a2 = -1.1; a1 = 0.5; a0 = -0.12; % коэффициенты полинома знаменателя ИПФ y = zeros(1,50); % резервирование памяти для хранения реакции u = ones(1,50); % единичное воздействиеym1 = 0; ym2 = 0; ym3 = 0 % начальные значения for i = 1:50 y(i) = a3*ym1; (7) ym1 = b2*u(i)-a2*y(i)+ym2; ym2 = b1*u(i)-a1*y(i)+ym3; ym3 = b0*u(i)-a0*y(i);end% График реакции дискретных моделей if 1 % Построение графиков figure (1) % активное окно графопостроителя clf % очистка предыдущих данных plot(y,'xb') % график y[n] m-файла hold on plot(out.ScopeData1.signals(3).values) % график y[n] Simulink модели, ver.1 plot(out.ScopeData1.signals(4).values) % график y[n] Simulink модели, ver.2 plot(out.ScopeData1.signals(5).values) % график y[n] Simulink модели, ver.3 plot(out.ScopeData1.signals(6).values) % график y[n] Simulink модели, ver.4 legend('m-file','Simulink v.1','Simulink v.2','Simulink v.3','Simulink v.4') grid xlabel('Номер отсчета') ylabel('Амплитуда реакции'), title('Сравнение реакций дискретных моделей') end  Рисунок 9. 100% совпадение реакций дискретных моделей и вычислений m-программы.  Рисунок 10. Варианты построения эквивалентных Simulink моделей рассматриваемого объекта. Порядок программирования динамических моделей контроллерами Для построения модели динамической системы средствами контроллеров предлагается выполнить следующее.
Рассмотренные варианты преобразования форм представления динамических моделей в интегрированной среде MATLAB могут быть использованы для реализации моделей средствами контроллеров путем построения кода эквивалентной импульсной передаточной функции (Рисунок 11).  Рисунок 11. Операторы MATLAB преобразования моделей и построения эквивалентного кода для программирования контроллеров. БИБЛИОГРАФИЧЕСКИЙ СПИСОК
=========== Источник: habr.com =========== Похожие новости:
Программирование ), #_matematika ( Математика ), #_matlab |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 15-Дек 00:23
Часовой пояс: UTC + 5
