[Алгоритмы, Программирование] Алгоритм Джонсона на орграфе с отрицательными дугами
Автор
Сообщение
news_bot ®
Стаж: 7 лет 11 месяцев
Сообщений: 27286
Статья подготовлена в преддверии старта курса «Алгоритмы и структуры данных»

Алгоритм Джонсона находит кратчайший путь между всеми парами вершин во взвешенном ориентированном графе с отрицательными весами без негативных контуров.
О, как звучит! Давайте разберём условие задачи по частям.
Граф, в котором каждое ребро имеет направление, называется ориентированным (или кратко – орграфом), а его рёбра называются дугами. Для примера, возьмём орграф из 4 вершин и 8 дуг:

Мы можем перемещаться из одной вершины в другую по дугам в указанном направлении. Перемещение по одной или нескольким дугам называется «путь» или «маршрут».
Для каждой дуги может быть указано число, которое называется «вес» или «длина» дуги. Мы будем смотреть на каждое число, как на длину. Цель алгоритма – найти кратчайший путь между любыми двумя вершинами. В качестве разминки, найдите кратчайший путь из вершины А в вершину D и напишите ответ в комментариях, а мы продолжим.
Вы, наверное, уже заметили, что некоторые дуги имеют отрицательный вес. Путешествие по таким дугам приносит доход. Мечтой путешественника было бы найти замкнутый путь с отрицательной длиной и ходить по нему вечно. Замкнутый путь называется «циклом» или «контуром», и если в орграфе есть такой негативный контур, то решение задачи отсутствует, так как минимальная длина пути может стремиться к минус бесконечности.
Итак, мы разобрали все термины условия, сформулируем цель алгоритма ещё раз, более осознанно:
Алгоритм Джонсона находит кратчайший путь между всеми парами вершин во взвешенном ориентированном графе с отрицательными весами без негативных контуров.
Для решения этой задачи можно применить алгоритм Флойда-Уоршелла, который решает задачу «в лоб» полным перебором:
for k = 1 to n // n – количество вершин в графе
for x = 1 to n
for y = 1 to n
W[x][y] = min(W[x][y], W[x][k] + W[k][y])
Значение W[x][y] элемента содержит длину кратчайшего пути из вершины х в вершину у.
Начальные значения для W – это матрица смежности исходного графа. Вместо нулей нужно записать плюс бесконечность, так как путь между такими вершинами ещё не найден.
Суть алгоритма в постоянном «релаксировании» длины маршрута. На каждой итерации мы пробуем попасть из X в Y через промежуточную вершину К, и если этот путь короче – запоминаем уменьшенную длину.
Алгоритм Флойда-Уоршелла перебирает все возможные варианты построения путей, сложность у него просто бомбическая – кубическая, и если в графе вершин много – он будет работать слишком долго.
Ещё есть эффективный алгоритм Дейкстры для поиска кратчайшего пути от одной вершины до всех остальных. Если применить алгоритм Дейкстры для каждой вершины, то мы получим кратчайшие пути для всех пар вершин, причём значительно быстрее, чем в алгоритме Флойда-Уоршелла.
Однако, алгоритм Дейкстры некорректно работает с графом с отрицательными весами.
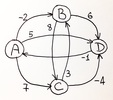
Например, при поиске от вершины А, на первом этапе будет найден кратчайший путь в вершину В (-2), а на втором этапе «кратчайшим» будет путь из В в D (-2+6=4). На этом алгоритм отрапартует о результате и закончит работу. Отрицательная дуга CD даже не будет рассмотрена и правильный ответ не будет найден.
Вот так. Один алгоритм медленный, другой некорректный.
Что же делать?
Ответ очевиден: использовать алгоритм Джонсона! Идея гениальна: на основе данного орграфа сформировать новый орграф таким образом, чтобы в нём не было отрицательных дуг, а все кратчайшие пути были такими же. Пропустить полученный орграф через алгоритм Дейкстры и на выходе получить верный ответ!
Как же нам сформировать такой орграф?
Простое неверное решение – увеличить длину каждой дуги на константное значение, чтобы отрицательных значений не осталось. Почему этот вариант некорректный? Потому что он даёт фору более коротким маршрутам, безосновательно увеличивая суммарную длину на ту самую константу с каждой новой дугой.
Например, если в предложенном графе длину каждой дуги увеличить на 4, то кратчайшим маршрутом из A в D станет прямой путь: 5 + 1 * 4 = 9. Тогда как правильный ответ из 3 дуг (A-B-C-D) получит лишних 12 грамм нагрузки и выпадет из конкуренции: -2 + 8 – 4 + 3 * 4 = 14.
Итак, наша задача – изменить длину каждой дуги таким образом, чтобы избавиться от отрицательных дуг и чтобы все кратчайшие расстояния остались такими же. Как это организовать? Давайте к длине каждой дуги XY добавим h(X) и вычтем h(Y), где h(v) – «чистая» функция, которая определяет некоторое константное значение для каждой вершины.
Получим такие длины дуг:



Посмотрим, как в этом случае изменится длина каждого маршрута из вершины A в D:

Как видим, любой путь из вершины A в D изменятся на одинаковую величину, h(A) – h(D), а, следовательно, все кратчайшие пути остаются такими же! Как раз то, что нужно.
Осталось теперь найти подходящие значения функции h, чтобы модифицированные длины дуг стали неотрицательными.
Рассмотрим, как можно рассчитать такие значения
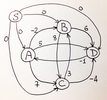
Для этого добавим в орграф новую вершину-исток S, из которой проведём нулевые дуги во все вершины графа. Обратим внимание, что добавление вершины S и дуг S* не изменяет кратчайших путей в исходном графе, потому как все добавленные дуги идут только из S, а «нулевого» маршрута в обратном направлении нет.
Теперь запустим алгоритм Беллмана-Форда, который найдёт кратчайшие пути от S до всех остальных вершин. Этот алгоритм N раз подряд перебирает все дуги на предмет «релаксации» кратчайших маршрутов из S во все остальные вершины. В таблице перечислены «значимые» итерации работы этого алгоритма, в каждом столбце указана очередная дуга, которая сокращает маршрут до одной из вершин:
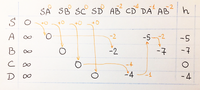
Результат работы этого алгоритма как раз и даст нам искомые значения функции h для каждой вершины. Суть этих значений – кратчайший путь из вершины S. Поскольку все дуги из S нулевые, то и значения функции h – неположительные. Но пусть это нас не смущает, главное, что полученные значения зафиксированы, не меняются, а, значит, мы можем пересчитать длины всех дуг исходного орграфа:

В итоге у нас получится орграф без отрицательных дуг:
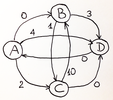
Здесь нет отрицательных дуг, а все кратчайшие маршруты такие же, как и в исходном орграфе, здорово! Теперь мы можем со спокойной душой запустить алгоритм Дейкстры на этом орграфе для каждой вершины и получить правильные ответы.
Посмотрим, как будут найдены кратчайшие маршруты из вершины А до всех остальных:
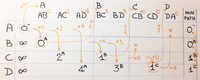
В каждом столбце, рядом с новым значением кратчайшего маршрута, записана вершина, откуда мы в неё пришли. По этим буквам мы можем восстановить кратчайший путь. Например, кратчайший маршрут из A в D восстанавливается по последнему столбцу и записывается справа налево: A <= B <= C <= D, что и требовалось найти.
итак, в этой статье мы рассмотрели идею алгоритма Джонсона на конкретном примере. Надеюсь, изучение этого алгоритма по Википедии теперь станет более понятным.
Узнать подробнее о курсе «Алгоритмы и структуры данных»
===========
Источник:
habr.com
===========
Похожие новости:
- [JavaScript, Программирование, Разработка веб-сайтов] 155 вопросов по JavaScript
- [Swift, Изучение языков, Программирование, Разработка мобильных приложений, Разработка под iOS] Делегаты и колбэки в Swift простым языком. Что же такое этот delegate, и как работает callback
- [Системное программирование, Программирование микроконтроллеров, Компьютерное железо] Делаем голову шинного USB-анализатора на базе комплекса Redd
- [Анализ и проектирование систем, Микросервисы, Программирование, Управление разработкой] Архитектура — Декларативна. Реализация — Императивна. Все остальное — Бюрократия
- [Интерфейсы, Программирование, Разработка веб-сайтов, Учебный процесс в IT] Задачи для фронтенд-тренировки: реализуем отдельные элементы интерфейсов YouTube, Instagram, Spotify, GitHub (перевод)
- [Разработка веб-сайтов, JavaScript, Программирование, ReactJS] Типичные ошибки джунов, использующих React (перевод)
- [Scala, Функциональное программирование] Определение серверной логики для конечной точки: три подхода (перевод)
- [Программирование, Тестирование IT-систем] Фрактальное тестирование
- [1С-Битрикс] Что должен уметь программист 1C?
- [Java, Kotlin] Производитель/потребитель на Kafka и Kotlin (перевод)
Теги для поиска: #_algoritmy (Алгоритмы), #_programmirovanie (Программирование), #_algoritm_dzhonsona (Алгоритм Джонсона), #_algoritm_flojdauorshella (Алгоритм Флойда-Уоршелла), #_algoritm_bellmanaforda (Алгоритм Беллмана-Форда), #_teorija_grafov (теория графов), #_orgraf (орграф), #_blog_kompanii_otus._onlajnobrazovanie (
Блог компании OTUS. Онлайн-образование
), #_algoritmy (
Алгоритмы
), #_programmirovanie (
Программирование
)
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 14-Янв 17:36
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 11 месяцев |
|
|
Статья подготовлена в преддверии старта курса «Алгоритмы и структуры данных»  Алгоритм Джонсона находит кратчайший путь между всеми парами вершин во взвешенном ориентированном графе с отрицательными весами без негативных контуров. О, как звучит! Давайте разберём условие задачи по частям. Граф, в котором каждое ребро имеет направление, называется ориентированным (или кратко – орграфом), а его рёбра называются дугами. Для примера, возьмём орграф из 4 вершин и 8 дуг:  Мы можем перемещаться из одной вершины в другую по дугам в указанном направлении. Перемещение по одной или нескольким дугам называется «путь» или «маршрут». Для каждой дуги может быть указано число, которое называется «вес» или «длина» дуги. Мы будем смотреть на каждое число, как на длину. Цель алгоритма – найти кратчайший путь между любыми двумя вершинами. В качестве разминки, найдите кратчайший путь из вершины А в вершину D и напишите ответ в комментариях, а мы продолжим. Вы, наверное, уже заметили, что некоторые дуги имеют отрицательный вес. Путешествие по таким дугам приносит доход. Мечтой путешественника было бы найти замкнутый путь с отрицательной длиной и ходить по нему вечно. Замкнутый путь называется «циклом» или «контуром», и если в орграфе есть такой негативный контур, то решение задачи отсутствует, так как минимальная длина пути может стремиться к минус бесконечности. Итак, мы разобрали все термины условия, сформулируем цель алгоритма ещё раз, более осознанно: Алгоритм Джонсона находит кратчайший путь между всеми парами вершин во взвешенном ориентированном графе с отрицательными весами без негативных контуров. Для решения этой задачи можно применить алгоритм Флойда-Уоршелла, который решает задачу «в лоб» полным перебором: for k = 1 to n // n – количество вершин в графе
for x = 1 to n for y = 1 to n W[x][y] = min(W[x][y], W[x][k] + W[k][y]) Значение W[x][y] элемента содержит длину кратчайшего пути из вершины х в вершину у. Начальные значения для W – это матрица смежности исходного графа. Вместо нулей нужно записать плюс бесконечность, так как путь между такими вершинами ещё не найден. Суть алгоритма в постоянном «релаксировании» длины маршрута. На каждой итерации мы пробуем попасть из X в Y через промежуточную вершину К, и если этот путь короче – запоминаем уменьшенную длину. Алгоритм Флойда-Уоршелла перебирает все возможные варианты построения путей, сложность у него просто бомбическая – кубическая, и если в графе вершин много – он будет работать слишком долго. Ещё есть эффективный алгоритм Дейкстры для поиска кратчайшего пути от одной вершины до всех остальных. Если применить алгоритм Дейкстры для каждой вершины, то мы получим кратчайшие пути для всех пар вершин, причём значительно быстрее, чем в алгоритме Флойда-Уоршелла. Однако, алгоритм Дейкстры некорректно работает с графом с отрицательными весами.  Например, при поиске от вершины А, на первом этапе будет найден кратчайший путь в вершину В (-2), а на втором этапе «кратчайшим» будет путь из В в D (-2+6=4). На этом алгоритм отрапартует о результате и закончит работу. Отрицательная дуга CD даже не будет рассмотрена и правильный ответ не будет найден. Вот так. Один алгоритм медленный, другой некорректный. Что же делать? Ответ очевиден: использовать алгоритм Джонсона! Идея гениальна: на основе данного орграфа сформировать новый орграф таким образом, чтобы в нём не было отрицательных дуг, а все кратчайшие пути были такими же. Пропустить полученный орграф через алгоритм Дейкстры и на выходе получить верный ответ! Как же нам сформировать такой орграф? Простое неверное решение – увеличить длину каждой дуги на константное значение, чтобы отрицательных значений не осталось. Почему этот вариант некорректный? Потому что он даёт фору более коротким маршрутам, безосновательно увеличивая суммарную длину на ту самую константу с каждой новой дугой. Например, если в предложенном графе длину каждой дуги увеличить на 4, то кратчайшим маршрутом из A в D станет прямой путь: 5 + 1 * 4 = 9. Тогда как правильный ответ из 3 дуг (A-B-C-D) получит лишних 12 грамм нагрузки и выпадет из конкуренции: -2 + 8 – 4 + 3 * 4 = 14. Итак, наша задача – изменить длину каждой дуги таким образом, чтобы избавиться от отрицательных дуг и чтобы все кратчайшие расстояния остались такими же. Как это организовать? Давайте к длине каждой дуги XY добавим h(X) и вычтем h(Y), где h(v) – «чистая» функция, которая определяет некоторое константное значение для каждой вершины. Получим такие длины дуг:    Посмотрим, как в этом случае изменится длина каждого маршрута из вершины A в D:  Как видим, любой путь из вершины A в D изменятся на одинаковую величину, h(A) – h(D), а, следовательно, все кратчайшие пути остаются такими же! Как раз то, что нужно. Осталось теперь найти подходящие значения функции h, чтобы модифицированные длины дуг стали неотрицательными. Рассмотрим, как можно рассчитать такие значения Для этого добавим в орграф новую вершину-исток S, из которой проведём нулевые дуги во все вершины графа. Обратим внимание, что добавление вершины S и дуг S* не изменяет кратчайших путей в исходном графе, потому как все добавленные дуги идут только из S, а «нулевого» маршрута в обратном направлении нет.  Теперь запустим алгоритм Беллмана-Форда, который найдёт кратчайшие пути от S до всех остальных вершин. Этот алгоритм N раз подряд перебирает все дуги на предмет «релаксации» кратчайших маршрутов из S во все остальные вершины. В таблице перечислены «значимые» итерации работы этого алгоритма, в каждом столбце указана очередная дуга, которая сокращает маршрут до одной из вершин:  Результат работы этого алгоритма как раз и даст нам искомые значения функции h для каждой вершины. Суть этих значений – кратчайший путь из вершины S. Поскольку все дуги из S нулевые, то и значения функции h – неположительные. Но пусть это нас не смущает, главное, что полученные значения зафиксированы, не меняются, а, значит, мы можем пересчитать длины всех дуг исходного орграфа:  В итоге у нас получится орграф без отрицательных дуг:  Здесь нет отрицательных дуг, а все кратчайшие маршруты такие же, как и в исходном орграфе, здорово! Теперь мы можем со спокойной душой запустить алгоритм Дейкстры на этом орграфе для каждой вершины и получить правильные ответы. Посмотрим, как будут найдены кратчайшие маршруты из вершины А до всех остальных:  В каждом столбце, рядом с новым значением кратчайшего маршрута, записана вершина, откуда мы в неё пришли. По этим буквам мы можем восстановить кратчайший путь. Например, кратчайший маршрут из A в D восстанавливается по последнему столбцу и записывается справа налево: A <= B <= C <= D, что и требовалось найти. итак, в этой статье мы рассмотрели идею алгоритма Джонсона на конкретном примере. Надеюсь, изучение этого алгоритма по Википедии теперь станет более понятным. Узнать подробнее о курсе «Алгоритмы и структуры данных» =========== Источник: habr.com =========== Похожие новости:
Блог компании OTUS. Онлайн-образование ), #_algoritmy ( Алгоритмы ), #_programmirovanie ( Программирование ) |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 14-Янв 17:36
Часовой пояс: UTC + 5
