[Python, Графический дизайн] Python, Треугольник Серпинского, и не только…
Автор
Сообщение
news_bot ®
Стаж: 7 лет 11 месяцев
Сообщений: 27286
Приветствую читателей. Это моя первая статья на Хабре. В ней я бы хотел поделиться своими экспериментами с алгоритмом построения фракталов путём размещения точек в определённых координатах.
Я не исключаю, что вы можете уже разбираться в теме фракталов, и даже работали с алгоритмом, о котором я буду рассказывать, и что информации об этом много, хоть я и не нашёл какие-то эксперименты с ним. Так что не бейте...
Начнём с рассказа о Треугольнике Серпинского. Это фрактал, то есть, как гласит ошибочная формулировка - само-подобная фигура, (чьи части подобны самой фигуре). Вы наверняка видели Треугольник Серпинского.
Треугольник СерпинскогоСуществует способ его создания, который мы и будем повторять на языке программирования Python. Сам алгоритм выглядит так:
Размещаем три угла.
Создаём строителя, который будет расположен на одном из трёх углов.
Повторяем вечно:
Перемещаем строителя в сторону случайного угла, но на половину пути.

Бирюзовый квадрат - это строитель.Эта картинка из программы, которую я написал на Python за пару минут. Использовал библиотеку pyxel, потому что она мне нравится, выглядит приятно, но как потом окажется - имеет недостаточное разрешение, что в нашем случае - сделает трудноразличимым маленькие элементы фрактала....
ФейлИ тут у меня возникла идея использовать четыре угла вместо трёх. Я ожидал, что получится такой же фрактал, только с четырёхугольниками (Ковёр Серпинского). Результат меня немного не порадовал - всё поле просто заполнялось точками хаотично, и не было никакого результата....
Строитель стремится к центру, немного колеблясьИ я ещё долгое время думал, что такой алгоритм будет работать только с треугольником. Но я ошибался, и совсем недавно решил, что надо делить путь до угла не на два, а на 3 или больше. Однако, это лишь смещало строителя в центр экрана. Но получился неплохой алгоритм проверки случайным чисел (Если точка переместилась в центр, и не выходит из него, значит - алгоритм случайных чисел хороший)....
Квадраты?И тут я решил идти в другую сторону, то есть делить путь до угла не на два, а на 1.n, например - на 1.75 Результат стал уже очень заметным. Что-то явно получается.Что, если использовать 5 углов, а делить ещё на меньшее число, например - 1.5 ?
Можно назвать это "Цветком Левина", в мою честь, если эту фигуру ещё никто не открыл?Однако, использовать настолько пиксельную библиотеку было плохим вариантом, поэтому я быстро вспомнил pygame, и переписал код уже на неё, так как там можно сделать 240 кадров в секунду, в надежде, что это ускорит процесс, а так же сделать разрешение экрана побольше, что, соответственно - улучшит детализацию.
Тест библиотеки pygameАлгоритм работает отлично. Значит - можно экспериментировать.
Применяем пять точек и деление на 1.75, чтобы получить наш цветок.

Пятиугольник-цветок тоже работает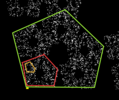
Если включить воображение, и преодолеть барьер восприятия в виде кучки пикселей, чему нас учил Майнкрафт - то можно увидеть, что эта фигура так же само-подобна....
Я даже попытался приблизить фрактал путём установки углов за границей экрана.К сожалению, фракталы почти не имеют практического предназначения, за исключением компьютерной графики, а мой цветок-шестиугольник вряд-ли будет выглядеть как-то красиво. Так что я принимаю тот факт, что "исследования" в этом направлении - не оправданы и бесполезны. Просто мне показалось это довольно интересной темой.Если кто-нибудь из вас владеет быстрым языком типа C++ или C# (Или Assembler?), и может оптимизировать программу настолько, насколько это возможно - то можете попробовать повторить эту программу, но добавив приближение фрактала, например - путём отрисовки установленных точек в координатах, относительных зуму, что можно реализовать через матрицу двумерного масштабирования, а точки записывать списком, чьи элементы состоят из векторов. У меня даже получилось сделать зум и передвижение по фракталу, правда, при масштабировании всё съезжает в правый нижний угол...
Надеюсь, вам было хоть немного интересно. Извиняюсь, если статья оказалась бесполезной/неинтересной, или показалась вам сырой. Большое спасибо вам за внимание.
===========
Источник:
habr.com
===========
Похожие новости:
- [Python, Программирование] Использование статистических методов для анализа временных рядов
- [Python, API] LongPoll в vk_api
- [Python, Машинное обучение] Оценка важности «фичей» для нелинейных моделей
- [Python, DevOps, Flask, Data Engineering] Развертывание нескольких моделей машинного обучения на одном сервере (перевод)
- [Python, Программирование] Как строить красивые графики на Python с Seaborn (перевод)
- [Python] 25 полезных однострочников Python, которые вы должны знать (перевод)
- [Python, Профессиональная литература] Книга «Секреты Python Pro»
- [Python, Программирование] Самая лучшая практика: работа с path в Python (перевод)
- [Python, Машинное обучение, Искусственный интеллект, TensorFlow] Нейродайджест: главное из области машинного обучения за январь 2021
- [Python] Оценка достоверности отчетов об ошибках с помощью анализа временных рядов
Теги для поиска: #_python, #_graficheskij_dizajn (Графический дизайн), #_python, #_fractal, #_fraktal (фрактал), #_python, #_graficheskij_dizajn (
Графический дизайн
)
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 15-Янв 11:48
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 11 месяцев |
|
|
Приветствую читателей. Это моя первая статья на Хабре. В ней я бы хотел поделиться своими экспериментами с алгоритмом построения фракталов путём размещения точек в определённых координатах. Я не исключаю, что вы можете уже разбираться в теме фракталов, и даже работали с алгоритмом, о котором я буду рассказывать, и что информации об этом много, хоть я и не нашёл какие-то эксперименты с ним. Так что не бейте...
 Треугольник СерпинскогоСуществует способ его создания, который мы и будем повторять на языке программирования Python. Сам алгоритм выглядит так: Размещаем три угла.
Создаём строителя, который будет расположен на одном из трёх углов. Повторяем вечно: Перемещаем строителя в сторону случайного угла, но на половину пути.  Бирюзовый квадрат - это строитель.Эта картинка из программы, которую я написал на Python за пару минут. Использовал библиотеку pyxel, потому что она мне нравится, выглядит приятно, но как потом окажется - имеет недостаточное разрешение, что в нашем случае - сделает трудноразличимым маленькие элементы фрактала....  ФейлИ тут у меня возникла идея использовать четыре угла вместо трёх. Я ожидал, что получится такой же фрактал, только с четырёхугольниками (Ковёр Серпинского). Результат меня немного не порадовал - всё поле просто заполнялось точками хаотично, и не было никакого результата....  Строитель стремится к центру, немного колеблясьИ я ещё долгое время думал, что такой алгоритм будет работать только с треугольником. Но я ошибался, и совсем недавно решил, что надо делить путь до угла не на два, а на 3 или больше. Однако, это лишь смещало строителя в центр экрана. Но получился неплохой алгоритм проверки случайным чисел (Если точка переместилась в центр, и не выходит из него, значит - алгоритм случайных чисел хороший)....  Квадраты?И тут я решил идти в другую сторону, то есть делить путь до угла не на два, а на 1.n, например - на 1.75 Результат стал уже очень заметным. Что-то явно получается.Что, если использовать 5 углов, а делить ещё на меньшее число, например - 1.5 ?  Можно назвать это "Цветком Левина", в мою честь, если эту фигуру ещё никто не открыл?Однако, использовать настолько пиксельную библиотеку было плохим вариантом, поэтому я быстро вспомнил pygame, и переписал код уже на неё, так как там можно сделать 240 кадров в секунду, в надежде, что это ускорит процесс, а так же сделать разрешение экрана побольше, что, соответственно - улучшит детализацию.  Тест библиотеки pygameАлгоритм работает отлично. Значит - можно экспериментировать. Применяем пять точек и деление на 1.75, чтобы получить наш цветок.
 Пятиугольник-цветок тоже работает  Если включить воображение, и преодолеть барьер восприятия в виде кучки пикселей, чему нас учил Майнкрафт - то можно увидеть, что эта фигура так же само-подобна....  Я даже попытался приблизить фрактал путём установки углов за границей экрана.К сожалению, фракталы почти не имеют практического предназначения, за исключением компьютерной графики, а мой цветок-шестиугольник вряд-ли будет выглядеть как-то красиво. Так что я принимаю тот факт, что "исследования" в этом направлении - не оправданы и бесполезны. Просто мне показалось это довольно интересной темой.Если кто-нибудь из вас владеет быстрым языком типа C++ или C# (Или Assembler?), и может оптимизировать программу настолько, насколько это возможно - то можете попробовать повторить эту программу, но добавив приближение фрактала, например - путём отрисовки установленных точек в координатах, относительных зуму, что можно реализовать через матрицу двумерного масштабирования, а точки записывать списком, чьи элементы состоят из векторов. У меня даже получилось сделать зум и передвижение по фракталу, правда, при масштабировании всё съезжает в правый нижний угол...  Надеюсь, вам было хоть немного интересно. Извиняюсь, если статья оказалась бесполезной/неинтересной, или показалась вам сырой. Большое спасибо вам за внимание. =========== Источник: habr.com =========== Похожие новости:
Графический дизайн ) |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 15-Янв 11:48
Часовой пояс: UTC + 5
