[Математика, Учебный процесс в IT, Научно-популярное] Второе место на Международной математической олимпиаде 2020
Автор
Сообщение
news_bot ®
Стаж: 7 лет 11 месяцев
Сообщений: 27286
Ура!
Сборная российских школьников заняла второе место!
Золотые медали завоевали Данила Демин из Сочи (36 баллов) и Алексей Львов из Новосибирска (36 баллов). Серебро взяли Иван Гайдай-Турлов (25), Антон Садовничий (29) из Москвы, Данил Сибгатуллин (29) из Москвы и Казани, а также Максим Туревский (30) из Петербурга.
Абсолютным победителем Олимпиады в личном зачете стал школьник из Китая Цзиньминь Ли (Jinmin Li), который набрал максимально возможные 42 балла.
Я недавно публиковал тексты задач и некоторые из них решили читатели Хабра в комментах.
Под катом немного интересной статистики по результатам олимпиады.

Наши молодцы!
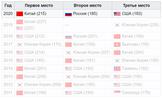
Командные результаты

Китай люто лидирует. Отрыв России от США в 2 очка.

Интересно, что у США руководитель с ярко выраженной азиатской фамилией, а зам. руководителя — с ярко выраженными украинскими именем и фамилией.
Индивидуальные результаты
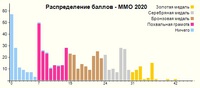

Китайские участники (1,2,3 места) с большим отрывом. 36 баллов (4 место) набрали представители многих стран.

Абсолютный чемпион Jinmin Li из города Чунцин. Респект.
Задачи

Задача 1
Внутри выпуклого четырёхугольника ABCD нашлась точка P, такая что выполняются равенства
∠PAD: ∠PBA: ∠DPA = 1: 2: 3 = ∠CBP: ∠BAP: ∠BPC.
Докажите, что следующие три прямые пересекаются в одной точке: внутренние биссектрисы углов ∠ADP и ∠PCB и серединный перпендикуляр к отрезку AB.
Задача 2
Даны вещественные числа a, b, c, d, такие что a > b > c > d > 0 и a + b + c + d = 1.
Докажите, что
(a + 2b + 3c + 4d) aabbccdd < 1.
Решение от novoselov тут
Задача 3
Имеется 4n камушков массами 1, 2, 3,..., 4n. Каждый из камушков покрашен в один из n цветов, причём имеется по 4 камушка каждого цвета.
Докажите, что камушки можно разделить на две кучи равного суммарного веса так, чтобы в каждой куче было по два камушка каждого цвета.
Решение от celen тут
Решение от novoselov тут
Задача 4
Дано целое число n > 1. На горном склоне расположено n2 фуникулёрных станций на разных высотах. Каждая из двух фуникулёрных компаний A и B владеет k подъёмниками. Каждый подъёмник осуществляет регулярный беспересадочный трансфер с одной из станций на другую, более высоко расположенную станцию. k трансферов компании A начинаются на k различных станциях; также они заканчиваются на k различных станциях; при этом трансфер, который начинается выше, и заканчивается выше. Те же условия выполнены для компании B. Будем говорить, что две станции связаны фуникулёрной компанией, если можно добраться из нижней станции в верхнюю, используя один или несколько трансферов данной компании (другие перемещения между станциями запрещены). Найдите наименьшее k, при котором заведомо найдутся две станции, связанные обеими компаниями.
Задача 5
Имеется n > 1 карточек, на каждой из которых написано целое положительное число.
Оказалось, что для любых двух карточек среднее арифметическое написанных на них чисел равно среднему геометрическому чисел, написанных на карточках некоторого набора, состоящего из одной или более карточек. При каких n из этого следует, что все числа, написанные на карточках, равны?
Решение от novoselov тут
Задача 6
Докажите, что существует положительная константа c, для которой выполняется следующее утверждение:
Пусть S — множество из n > 1 точек плоскости, в котором расстояние между любыми двумя точками не меньше 1. Тогда существует прямая ℓ, разделяющая множество S, такая что расстояние от любой точки S до ℓ не меньше чем cn−1/3.
(Прямая ℓ разделяет множество точек S, если она пересекает некоторый отрезок, концы которого принадлежат S.)
Замечание. Более слабые результаты с заменой cn−1/3 на cn−α могут оцениваться в зависимости от значения константы α > 1/3.

Статистика решения 6й задачи. Китайцы показали себя отлично. С хорошим результатом и француз Владимир Иванов.
===========
Источник:
habr.com
===========
Похожие новости:
- [Учебный процесс в IT, Карьера в IT-индустрии] Mail.ru Group, МФТИ и МГТУ им. Н. Э. Баумана проведут международную олимпиаду по программированию для школьников
- [Научно-популярное, Физика] Природа даёт подсказку, как двигаться быстрее скорости света
- [Интерфейсы, Карьера в IT-индустрии, Лайфхаки для гиков, Учебный процесс в IT] Как начать понимать на слух английский? Подружиться с умными колонками
- [Научно-популярное, Космонавтика] Сентябрь. Считаем запуски — «Китай впереди»
- [Биотехнологии, Здоровье, Мозг, Научная фантастика, Научно-популярное] Крионика — последняя надежда на смерть?
- [Будущее здесь, Космонавтика, Научно-популярное] После замера радиации на Луне ученые предложили строить базу под ее поверхностью
- [Учебный процесс в IT, Карьера в IT-индустрии, IT-компании] Студенческие IT стажировки — как мы стараемся делать их наиболее эффективными
- [Python, Математика, Машинное обучение, Научно-популярное, Мозг] Новый способ изучения психотропных веществ с помощью ЭЭГ и нейронных сетей
- [Программирование, Алгоритмы, Научно-популярное] Можно ли научить обезьяну программировать? Ждёт ли нас поколение специалистов-бабуинов
- [Научно-популярное, Биотехнологии, Химия, Экология] Искра жизни: теория зарождения первой органики
Теги для поиска: #_matematika (Математика), #_uchebnyj_protsess_v_it (Учебный процесс в IT), #_nauchnopopuljarnoe (Научно-популярное), #_matematika (математика), #_olimpiada (олимпиада), #_matematika (
Математика
), #_uchebnyj_protsess_v_it (
Учебный процесс в IT
), #_nauchnopopuljarnoe (
Научно-популярное
)
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 14-Янв 17:36
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 11 месяцев |
|
 Ура! Сборная российских школьников заняла второе место! Золотые медали завоевали Данила Демин из Сочи (36 баллов) и Алексей Львов из Новосибирска (36 баллов). Серебро взяли Иван Гайдай-Турлов (25), Антон Садовничий (29) из Москвы, Данил Сибгатуллин (29) из Москвы и Казани, а также Максим Туревский (30) из Петербурга. Абсолютным победителем Олимпиады в личном зачете стал школьник из Китая Цзиньминь Ли (Jinmin Li), который набрал максимально возможные 42 балла. Я недавно публиковал тексты задач и некоторые из них решили читатели Хабра в комментах. Под катом немного интересной статистики по результатам олимпиады.  Наши молодцы! Командные результаты  Китай люто лидирует. Отрыв России от США в 2 очка.  Интересно, что у США руководитель с ярко выраженной азиатской фамилией, а зам. руководителя — с ярко выраженными украинскими именем и фамилией. Индивидуальные результаты   Китайские участники (1,2,3 места) с большим отрывом. 36 баллов (4 место) набрали представители многих стран.  Абсолютный чемпион Jinmin Li из города Чунцин. Респект. Задачи  Задача 1 Внутри выпуклого четырёхугольника ABCD нашлась точка P, такая что выполняются равенства ∠PAD: ∠PBA: ∠DPA = 1: 2: 3 = ∠CBP: ∠BAP: ∠BPC. Докажите, что следующие три прямые пересекаются в одной точке: внутренние биссектрисы углов ∠ADP и ∠PCB и серединный перпендикуляр к отрезку AB. Задача 2 Даны вещественные числа a, b, c, d, такие что a > b > c > d > 0 и a + b + c + d = 1. Докажите, что (a + 2b + 3c + 4d) aabbccdd < 1. Решение от novoselov тут Задача 3 Имеется 4n камушков массами 1, 2, 3,..., 4n. Каждый из камушков покрашен в один из n цветов, причём имеется по 4 камушка каждого цвета. Докажите, что камушки можно разделить на две кучи равного суммарного веса так, чтобы в каждой куче было по два камушка каждого цвета. Решение от celen тут Решение от novoselov тут Задача 4 Дано целое число n > 1. На горном склоне расположено n2 фуникулёрных станций на разных высотах. Каждая из двух фуникулёрных компаний A и B владеет k подъёмниками. Каждый подъёмник осуществляет регулярный беспересадочный трансфер с одной из станций на другую, более высоко расположенную станцию. k трансферов компании A начинаются на k различных станциях; также они заканчиваются на k различных станциях; при этом трансфер, который начинается выше, и заканчивается выше. Те же условия выполнены для компании B. Будем говорить, что две станции связаны фуникулёрной компанией, если можно добраться из нижней станции в верхнюю, используя один или несколько трансферов данной компании (другие перемещения между станциями запрещены). Найдите наименьшее k, при котором заведомо найдутся две станции, связанные обеими компаниями. Задача 5 Имеется n > 1 карточек, на каждой из которых написано целое положительное число. Оказалось, что для любых двух карточек среднее арифметическое написанных на них чисел равно среднему геометрическому чисел, написанных на карточках некоторого набора, состоящего из одной или более карточек. При каких n из этого следует, что все числа, написанные на карточках, равны? Решение от novoselov тут Задача 6 Докажите, что существует положительная константа c, для которой выполняется следующее утверждение: Пусть S — множество из n > 1 точек плоскости, в котором расстояние между любыми двумя точками не меньше 1. Тогда существует прямая ℓ, разделяющая множество S, такая что расстояние от любой точки S до ℓ не меньше чем cn−1/3. (Прямая ℓ разделяет множество точек S, если она пересекает некоторый отрезок, концы которого принадлежат S.) Замечание. Более слабые результаты с заменой cn−1/3 на cn−α могут оцениваться в зависимости от значения константы α > 1/3.  Статистика решения 6й задачи. Китайцы показали себя отлично. С хорошим результатом и француз Владимир Иванов. =========== Источник: habr.com =========== Похожие новости:
Математика ), #_uchebnyj_protsess_v_it ( Учебный процесс в IT ), #_nauchnopopuljarnoe ( Научно-популярное ) |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 14-Янв 17:36
Часовой пояс: UTC + 5
