[Open source, Python, Data Mining, Big Data] Crime, Race and Lethal Force in the USA — Part 3 (перевод)
Автор
Сообщение
news_bot ®
Стаж: 7 лет 11 месяцев
Сообщений: 27286
This is the concluding part of my article devoted to a statistical analysis of police shootings and criminality among the white and the black population of the United States. In the first part, we talked about the research background, goals, assumptions, and source data; in the second part, we investigated the national use-of-force and crime data and tracked their connection with race.
Let's recall the intermediate inferences that we were able to make from the available data for 2000 — 2018:
- White police victims outnumber black victims in absolute figures.
- Use of lethal force results in an average of 5.9 per one million Black deaths and 2.3 per one million White deaths (Black victim count is 2.6 greater in unit values).
- Year-to-year scatter in Black lethal force fatalities is nearly twice the scatter in White fatalities.
- White fatalities grow continuously from year to year (by 0.1 — 0.2 per million on average), while Black fatalities rolled back to their 2009 level after climaxing in 2011 — 2013.
- Whites commit twice as many offenses as Blacks in absolute numbers, but three times as fewer in per capita numbers (per 1 million population within that race).
- Criminality among Whites grows more or less steadily over the entire period of investigation (doubled over 19 years). Criminality among Blacks also grows, but by leaps and starts; over the entire period, however, the growth factor is also 2, like with Whites.
- Fatal encounters with law enforcement are connected with criminality (number of offenses committed). The correlation though differs between the two races: for Whites, it is almost perfect, for Blacks — far from perfect.
- Lethal force victims grow 'in reply to' criminality growth, generally with a few years' lag (this is more conspicuous in the Black data).
- White offenders tend to meet death from the police a little more frequently than Black offenders.
Today, as I promised, we'll be looking at the geographical distribution of these data across the states, which ought to either confirm or confute the previous conclusions.
However, before we take up geography, let's make a step back and see what happens if we analyze only the most violent offenses instead of 'All Offenses' as the source data for criminality. Many of my readers have pointed out in their comments that this would have been more proper, since 'All Offenses' incorporate those which should not (in practice) be associated with aggressive behavior provoking police shooting, such as petty larceny or selling drugs. I cannot whole-heartedly agree with this reasoning because, as I see it, any offense can arouse or heighten attention from the law enforcement, which in turn may wind up sadly… Still, let's just be curious enough to check!
Assault and Murder Instead of All Offenses
We just need to change one line of code where we form the crime dataset. Replace this line
df_crimes1 = df_crimes1.loc[df_crimes1['Offense'] == 'All Offenses']
with this:
df_crimes1 = df_crimes1.loc[df_crimes1['Offense'].str.contains('Assault|Murder')]
Our new filter now lets through only offenses connected with assault (simple and aggravated) and murder / non-negligent homicide (negligent / justifiable homicide / manslaughter cases are not included).
We leave the rest of the code as it was.
The number of crimes per 1 million population within each race now looks as follows:

We can see that, though the scale (Y-axis) is much lower, the shape of the curves is almost identical to the All Offenses ones we saw previously.
The criminality vs. lethal force victims curves for both races:


And the correlation matrix:
White_promln_cr
White_promln_uof
Black_promln_cr
Black_promln_uof
White_promln_cr
1.000000
0.684757
0.986622
0.729674
White_promln_uof
0.684757
1.000000
0.614132
0.795486
Black_promln_cr
0.986622
0.614132
1.000000
0.680893
Black_promln_uof
0.729674
0.795486
0.680893
1.000000
The correlation between criminality and lethal force fatalities is worse this time (0.68 against 0.88 and 0.72 for All Offenses). But the silver lining here is the fact that the correlation coefficients for Whites and Blacks are almost equal, which gives reason to say there is some constant correlation between crime and police shootings / victims (regardless of race).
Now for our 'DIY' index — the ratio of lethal force deaths to the number of crimes (both per capita):

The difference here is even more apparent. The inference is the same: White criminals are more likely to get killed by the police than Black criminals.
The summary is that all our prior conclusions hold true.
Well, down to geography lessons now! :)
Source Data
To investigate criminality in individual states, I used different source endpoints in the FBI database:
- State level UCR Estimated Crime Data Endpoint — without race classification (the resulting CSV can be downloaded from here)
- State level Arrest Demographic Count By Offense Endpoint — with race classification (the resulting CSV can be downloaded from here)
Unfortunately, I didn't manage to get complete data on committed offenses with the offense state, year and offender race, much as I tried. The returned results had large gaps, for example, some states were totally omitted. But the alternative data on arrests is quite sufficient for our humble research.
The first dataset contains crime counts for all the 51 states from 1991 to 2018, for the following offense categories:
- violent crime (murder, rape, robbery and aggravated assault)
- homicide (all types, including negligent / justifiable)
- rape legacy (using outdated metrics — before 2013)
- rape revised (using updated metrics — from 2013 on)
- robbery
- aggravated assault
- property crime
- burglary
- larceny
- motor vehicle theft
- arson
For our purposes, we'll be using the 'violent crime' category, in keeping with the rest of the research.
The second dataset features the number of arrests for the 51 states from 2000 to 2018, with details on the arrested persons' race (refer to the previous part for the race categories). Since the arrest dataset uses a different offense classification and doesn't provide the combined 'violent crime' category, the requests and retrieved results are for the four constituent offenses — murder / non-negligent manslaughter, robbery, rape, and aggravated assault.
Crime Distribution (No Racial Factor)
First, we'll look at the distribution of violent crimes across the states regardless of the offenders' race:
import pandas as pd, numpy as np
CRIME_STATES_FILE = ROOT_FOLDER + '\\crimes_by_state.csv'
df_crime_states = pd.read_csv(CRIME_STATES_FILE, sep=';', header=0,
usecols=['year', 'state_abbr', 'population', 'violent_crime'])
The resulting dataset:
year
state_abbr
population
violent_crime
0
2016
AL
4860545
25878
1
1996
AL
4273000
24159
2
1997
AL
4319000
24379
3
1998
AL
4352000
22286
4
1999
AL
4369862
21421
...
...
...
...
...
1423
2000
DC
572059
8626
1424
2001
DC
573822
9195
1425
2002
DC
569157
9322
1426
2003
DC
557620
9061
1427
2016
DC
684336
8236
1428 rows × 4 columns
Adding the full state names (the list of states we already used in our research — CSV) and optimizing / sorting the data:
df_crime_states = df_crime_states.merge(df_state_names, on='state_abbr')
df_crime_states.dropna(inplace=True)
df_crime_states.sort_values(by=['year', 'state_abbr'], inplace=True)
Since the dataset already has population values, let's calculate the number of crimes per million people:
df_crime_states['crime_promln'] = df_crime_states['violent_crime'] * 1e6 /
df_crime_states['population']
Finally, we'll turn the data into a table spanning the 2000 — 2018 period transposing the state names and dropping the redundant columns:
df_crime_states_agg = df_crime_states.groupby(['state_name',
'year'])['violent_crime'].sum().unstack(level=1).T
df_crime_states_agg.fillna(0, inplace=True)
df_crime_states_agg = df_crime_states_agg.astype('uint32').loc[2000:2018, :]
The resulting table contains 19 rows (year observations from 2000 through 2018) and 51 columns (by the number of states).
Let's display the top 10 states for the average number of crimes:
df_crime_states_agg_top10 = df_crime_states_agg.describe().T.nlargest(10, 'mean').\
astype('uint32')
count
mean
std
min
25%
50%
75%
max
state_name
California
19
181514
19425
153763
165508
178597
193022
212867
Texas
19
117614
6522
104734
113212
121091
122084
126018
Florida
19
110104
18542
81980
92809
113541
127488
131878
New York
19
81618
9548
68495
75549
77563
85376
105111
Illinois
19
62866
10445
47775
54039
64185
69937
81196
Michigan
19
49273
5029
41712
44900
49737
54035
56981
Pennsylvania
19
46941
5066
39192
41607
48188
51021
55028
Tennessee
19
41951
2432
38063
40321
41562
43358
46482
Georgia
19
40228
3327
34355
38283
39435
41495
47353
North Carolina
19
37936
3193
32718
34706
38243
40258
43125
We'll also make it more graphic with a box plot:
df_crime_states_top10 = df_crime_states_agg.loc[:, df_crime_states_agg_top10.index]
plt = df_crime_states_top10.plot.box(figsize=(12, 10))
plt.set_ylabel('Violent crime count (2000 - 2018)')

The 'Hollywood' state easily and notoriously beats the rest 9. The 'prizewinners' are California, Texas and Florida, all three in the South, the regular settings for most Hollywood criminal blockbusters.
You can also see that criminality has changed considerably over the observed period in some states (California, Florida and Illinois), whereas in others (like Georgia) it has remained almost constant.
I tend to think the crime rates are in some way connected with population :) Let's see the top 10 states by population in 2018:
df_crime_states_2018 = df_crime_states.loc[df_crime_states['year'] == 2018]
plt = df_crime_states_2018.nlargest(10, 'population').\
sort_values(by='population').plot.barh(x='state_name',
y='population', legend=False, figsize=(10,5))
plt.set_xlabel('2018 Population')
plt.set_ylabel('')
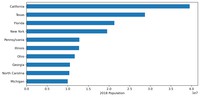
Same old mugs here :) Let's check the correlation between crimes and population:
df_corr = df_crime_states[df_crime_states['year']>=2000].groupby(['state_name']).mean()
df_corr = df_corr.loc[:, ['population', 'violent_crime']]
df_corr.corr(method='pearson').at['population', 'violent_crime']
The calculated Pearson correlation coefficient is 0.98. Q.E.D.
But the per capita crime counts give a staringly different picture:
plt = df_crime_states_2018.nlargest(10, 'crime_promln').\
sort_values(by='crime_promln').plot.barh(x='state_name',
y='crime_promln', legend=False, figsize=(10,5))
plt.set_xlabel('Number of violent crimes per 1 mln. population (2018)')
plt.set_ylabel('')
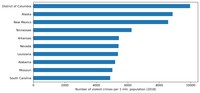
There's a pretty kettle of fish! The leaders by per capita crimes are the least populated states: District Columbia (with the US capital) and Alaska (both home to some 700+ thousand people as of 2018), as well as one medium-populated state — New Mexico, with 2 mln. people. Only one state from our previous toplist is featured here — Tennessee, which gives this state a less-than-desirable reputation.
We will then display these results on the US map. To do this, we need the folium library:
import folium
First, the 2018 absolute crime counts:
FOLIUM_URL = 'https://raw.githubusercontent.com/python-visualization/folium/master/examples/data'
FOLIUM_US_MAP = f'{FOLIUM_URL}/us-states.json'
m = folium.Map(location=[48, -102], zoom_start=3)
folium.Choropleth(
geo_data=FOLIUM_US_MAP,
name='choropleth',
data=df_crime_states_2018,
columns=['state_abbr', 'violent_crime'],
key_on='feature.id',
fill_color='YlOrRd',
fill_opacity=0.7,
line_opacity=0.2,
legend_name='Violent crimes in 2018',
bins=df_crime_states_2018['violent_crime'].quantile(
list(np.linspace(0.0, 1.0, 5))).to_list(),
reset=True
).add_to(m)
folium.LayerControl().add_to(m)
m

The same in per capita values (per 1 million):
m = folium.Map(location=[48, -102], zoom_start=3)
folium.Choropleth(
geo_data=FOLIUM_US_MAP,
name='choropleth',
data=df_crime_states_2018,
columns=['state_abbr', 'crime_promln'],
key_on='feature.id',
fill_color='YlOrRd',
fill_opacity=0.7,
line_opacity=0.2,
legend_name='Violent crimes in 2018 (per 1 mln. population)',
bins=df_crime_states_2018['crime_promln'].quantile(
list(np.linspace(0.0, 1.0, 5))).to_list(),
reset=True
).add_to(m)
folium.LayerControl().add_to(m)
m

In the first case, as we can see, crimes are more or less evenly distributed in the North to South direction. In the second case, it's mostly the Southern states plus DC and Alaska that make the trend.
Lethal Force Fatalities Across States (No Racial Factor)
We are now going to look at lethal force used in individual states across the country.
To prepare the dataset, we'll complement the UOF (Use Of Force) data we used previously by the full state names, group the cases by states, and constrain the observations to years 2000 through 2018:
df_fenc_agg_states = df_fenc.merge(df_state_names, how='inner',
left_on='State', right_on='state_abbr')
df_fenc_agg_states.fillna(0, inplace=True)
df_fenc_agg_states = df_fenc_agg_states.rename(columns={'state_name_x': 'State Name'})
df_fenc_agg_states = df_fenc_agg_states.loc[:, ['Year', 'Race', 'State',
'State Name', 'Cause', 'UOF']]
df_fenc_agg_states = df_fenc_agg_states.\
groupby(['Year', 'State Name', 'State'])['UOF'].\
count().unstack(level=0)
df_fenc_agg_states.fillna(0, inplace=True)
df_fenc_agg_states = df_fenc_agg_states.astype('uint16').loc[:, :2018]
df_fenc_agg_states = df_fenc_agg_states.reset_index()
Top 10 states for police victims in 2018:
df_fenc_agg_states_2018 = df_fenc_agg_states.loc[:, ['State Name', 2018]]
plt = df_fenc_agg_states_2018.nlargest(10, 2018).sort_values(2018).plot.barh(
x='State Name', y=2018, legend=False, figsize=(10,5))
plt.set_xlabel('Number of UOF victims in 2018')
plt.set_ylabel('')
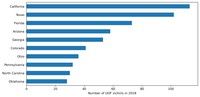
Let's also review the data for the entire period as a box plot:
fenc_top10 = df_fenc_agg_states.loc[df_fenc_agg_states['State Name'].\
isin(df_fenc_agg_states_2018.nlargest(10, 2018)['State Name'])]
fenc_top10 = fenc_top10.T
fenc_top10.columns = fenc_top10.loc['State Name', :]
fenc_top10 = fenc_top10.reset_index().loc[2:, :].set_index('Year')
df_sorted = fenc_top10.mean().sort_values(ascending=False)
fenc_top10 = fenc_top10.loc[:, df_sorted.index]
plt = fenc_top10.plot.box(figsize=(12, 6))
plt.set_ylabel('Number of UOF victims (2000 - 2018)')

Yep! The same 'unholy trio' of California, Texas and Florida, with their other two Southern sidekicks — Arizona and Georgia. The leaders again show large scatter indicative of year-to-year changes.
Connection Between Lethal Force Fatalities and Crimes
As in the previous part of this research, we are investigating the possible connection between criminality and deaths at the hands of law enforcement. We'll start without the racial factor, to see if such a connection exists in principle and how it varies from state to state.
At first, we must merge the UOF and (violent) crime datasets, setting the observation period to 2000 — 2018:
# add full state names
df_fenc_crime_states = df_fenc.merge(df_state_names, how='inner',
left_on='State', right_on='state_abbr')
# rename some columns
df_fenc_crime_states = df_fenc_crime_states.rename(columns={'Year': 'year',
'state_name_x': 'state_name'})
# truncate period to 2000-2018
df_fenc_crime_states = df_fenc_crime_states[df_fenc_crime_states['year'].between(2000,
2018)]
# group by year and state
df_fenc_crime_states = df_fenc_crime_states.groupby(['year', 'state_name'])['UOF'].\
count().reset_index()
# join with crime data
df_fenc_crime_states = df_fenc_crime_states.merge(df_crime_states[df_crime_states['year'].\
between(2000, 2018)], how='outer', on=['year', 'state_name'])
# set missing data to zero
df_fenc_crime_states.fillna({'UOF': 0}, inplace=True)
# unify data types
df_fenc_crime_states = df_fenc_crime_states.astype({'year': 'uint16', 'UOF': 'uint16',
'population': 'uint32', 'violent_crime': 'uint32'})
# sort data
df_fenc_crime_states = df_fenc_crime_states.sort_values(by=['year', 'state_name'])
Resulting dataset
SPL
year
state_name
UOF
state_abbr
population
violent_crime
crime_promln
0
2000
Alabama
7
AL
4447100
21620
4861.595197
1
2000
Alaska
2
AK
626932
3554
5668.876369
2
2000
Arizona
11
AZ
5130632
27281
5317.278651
3
2000
Arkansas
4
AR
2673400
11904
4452.756789
4
2000
California
97
CA
33871648
210531
6215.552311
...
...
...
...
...
...
...
...
907
2018
Virginia
18
VA
8517685
17032
1999.604353
908
2018
Washington
24
WA
7535591
23472
3114.818732
909
2018
West Virginia
7
WV
1805832
5236
2899.494527
910
2018
Wisconsin
10
WI
5813568
17176
2954.467893
911
2018
Wyoming
4
WY
577737
1226
2122.072846
As you will remember, the UOF column contains the number of deaths from encounters with law enforcement officers (who I sometimes call here just 'the police', but who include, of course, other agencies such as the FBI) where lethal force was used intentionally.
We will also make a separate dataset with year-average values:
df_fenc_crime_states_agg = df_fenc_crime_states.groupby(['state_name']).\
mean().loc[:, ['UOF', 'violent_crime']]
Now let's look at the year averages for crimes and lethal force fatalities for all the 51 states on one plot:
plt = df_fenc_crime_states_agg['violent_crime'].plot.bar(legend=True, figsize=(15,5))
plt.set_ylabel('Number of violent crimes (year average)')
plt2 = df_fenc_crime_states_agg['UOF'].plot(secondary_y=True, style='g', legend=True)
plt2.set_ylabel('Number of UOF victims (year average)', rotation=90)
plt2.set_xlabel('')
plt.set_xlabel('')
plt.set_xticklabels(df_fenc_crime_states_agg.index, rotation='vertical')
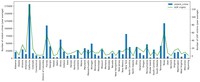
Looking closely at this combined chart, one can see the following:
- the connection between crime and use of force is plainly trackable: the green UOF curve tends to repeat the shape of the crime bars
- the more criminal states (such as Florida, Illinois, Michigan, New York and Texas) evince proportionately less use of force compared to the less criminal states
Let's also make a scatterplot:
plt = df_fenc_crime_states_agg.plot.scatter(x='violent_crime', y='UOF')
plt.set_xlabel('Number of violent crimes (year average)')
plt.set_ylabel('Number of UOF victims (year average)')

Here it becomes conspicuous that the ratio between crime and use of lethal force is affected by the crime rate. Speaking crudely, in states with the number of violent crimes below 75k the number of police victims grows more slowly; whereas in the states with the crime count above 75k this growth is quite steep. This latter group includes, as we can see, only four states. Let's look them 'in the face':
df_fenc_crime_states_agg[df_fenc_crime_states_agg['violent_crime'] > 75000]
UOF
violent_crime
state_name
California
133.263158
181514.578947
Florida
54.578947
110104.315789
New York
19.157895
81618.052632
Texas
64.368421
117614.631579
Will you be surprised? We've got the same 'four horsemen of the Apocalypse': California, Florida, Texas and New York.
Correspondingly, let's calculate the correlation coefficients between our data for three cases:
- states with the year average crime count up to 75,000
- states with the year average crime count above 75,000
- all the states
For the first case:
df_fenc_crime_states_agg[df_fenc_crime_states_agg['violent_crime'] <= \
75000].corr(method='pearson').at['UOF', 'violent_crime']
— we obtain 0.839 as the correlation coefficient. This is a statistically valid value, although it doesn't reach 0.9 due to scatter across the 47 states.
For the first case:
df_fenc_crime_states_agg[df_fenc_crime_states_agg['violent_crime'] > \
75000].corr(method='pearson').at['UOF', 'violent_crime']
— we get 0.999 — an ideal correlation!
For the last case (all states):
df_fenc_crime_states_agg.corr(method='pearson').at['UOF', 'violent_crime']
— the correlation is estimated at 0.935. This overall correlation may be considered very good.
Let's now look at the geographical distribution of our 'offender shootdown' index (the term is coined here for brevity). As before, we divide the number of lethal force fatalities by the number of crimes:
df_fenc_crime_states_agg['uof_by_crime'] = df_fenc_crime_states_agg['UOF'] /
df_fenc_crime_states_agg['violent_crime']
plt = df_fenc_crime_states_agg.loc[:, 'uof_by_crime'].sort_values(ascending=False).\
plot.bar(figsize=(15,5))
plt.set_xlabel('')
plt.set_ylabel('Ratio of UOF victims to number of violent crimes')
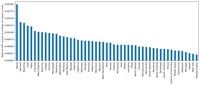
It is interesting to observe that our erstwhile leaders have shifted toward the center or even the rightmost end of the chart, which must mean that the most criminal states don't have the most 'bloodthirsty' police (towards real or potential offenders).
Intermediate conclusions:
- The number of violent crimes is directly proportionate to population (good call, Captain Obvious!)
- The most populated states (California, Florida, Texas and New York) are also the most criminal, in absolute values.
- In per capita values, Southern states are more criminal than Northern states, with the exception of Alaska and District Columbia.
- Lethal force deaths are correlated to criminality with an average coefficient of 0.93 across all the states. This correlation reaches almost unity (strictly linear) for the most criminal states and only 0.84 for the rest.
Racial Factor in Criminality and Lethal Force Fatalities Across States
Proving that crime rates do affect police victim rates, let's add the racial factor and see what it affects. As I explained above, we'll be using the arrest data for this purpose as being the most complete and covering the main offenses for all the states. There is, of course, no such state or country where one could equate the number of committed crimes to the number of arrests; yet these parameters are closely related. As such, we can do very well with arrest data for our statistical analysis. And, as we already agreed, only violent offenses (murder, rape, robbery, aggravated assault) will be taken into account.
Let's load the source data from the CSV file and routinely add the full state names:
ARRESTS_FILE = ROOT_FOLDER + '\\arrests_by_state_race.csv'
# arrests of Blacks and Whites only
df_arrests = pd.read_csv(ARRESTS_FILE, sep=';', header=0,
usecols=['data_year', 'state', 'white', 'black'])
# sum the four offenses and group by states
df_arrests = df_arrests.groupby(['data_year', 'state']).sum().reset_index()
# add state names
df_arrests = df_arrests.merge(df_state_names, left_on='state', right_on='state_abbr')
# rename / remove columns
df_arrests = df_arrests.rename(columns={'data_year': 'year'}).drop(columns='state_abbr')
# peek at the result
df_arrests.head()
year
state
black
white
state_name
0
2000
AK
140
613
Alaska
1
2001
AK
139
718
Alaska
2
2002
AK
143
677
Alaska
3
2003
AK
173
801
Alaska
4
2004
AK
163
765
Alaska
We'll also create a dataframe with year average values:
df_arrests_agg = df_arrests.groupby(['state_name']).mean().drop(columns='year')
Arrests of Whites and Blacks in 51 states (year average counts)
SPL
black
white
state_name
Alabama
2805.842105
1757.315789
Alaska
221.894737
844.157895
Arizona
1378.368421
7007.157895
Arkansas
2387.894737
2303.789474
California
26668.368421
87252.315789
Colorado
1268.210526
5157.368421
Connecticut
2097.631579
2981.210526
Delaware
1356.894737
1048.578947
District of Columbia
111.111111
4.944444
Florida
12.000000
7.000000
Georgia
8262.842105
3502.894737
Hawaii
81.052632
368.736842
Idaho
44.000000
1362.263158
Illinois
5699.842105
1841.894737
Indiana
3553.368421
5192.263158
Iowa
1104.421053
3039.473684
Kansas
522.315789
1501.315789
Kentucky
1476.894737
1906.052632
Louisiana
5928.789474
3414.263158
Maine
63.736842
699.526316
Maryland
7189.105263
4010.684211
Massachusetts
3407.157895
7319.684211
Michigan
7628.157895
6304.157895
Minnesota
2231.210526
2645.736842
Mississippi
1462.210526
474.368421
Missouri
5777.473684
5703.368421
Montana
27.684211
673.684211
Nebraska
591.421053
1058.526316
Nevada
1956.421053
3817.210526
New Hampshire
68.368421
640.789474
New Jersey
6424.157895
6043.789474
New Mexico
234.421053
2809.368421
New York
8394.526316
8734.947368
North Carolina
10527.947368
7412.947368
North Dakota
61.263158
277.052632
Ohio
4063.947368
4071.368421
Oklahoma
1625.105263
3353.000000
Oregon
445.105263
3373.368421
Pennsylvania
11974.157895
11039.473684
Rhode Island
275.684211
699.210526
South Carolina
5578.526316
3615.421053
South Dakota
67.105263
349.368421
Tennessee
6799.894737
8462.526316
Texas
10547.631579
22062.684211
Utah
167.105263
1748.894737
Vermont
43.526316
439.210526
Virginia
4100.421053
3060.263158
Washington
1688.947368
6012.105263
West Virginia
271.263158
1528.315789
Wisconsin
3440.055556
4107.722222
Wyoming
27.263158
506.947368
Looking at this table, one can't overlook some oddities. In some states the arrest counts reach hundreds and thousands, while in others — only dozens or fewer. That's the case with Florida, one of the most populated states: it counts only 19 arrests per year (12 Blacks and 7 Whites). Surely, some data is missing here; let's check:
df_arrests[df_arrests['state'] == 'FL']
And indeed we see that data for Florida is available only for 2017. Well, we'll have to put up with this, I suppose. All the other states have complete data. But the ten / hundred-fold difference should be accounted for by population. Let's add population-by-race data and have a look.
The population data was taken from the US Census Bureau website (which is for some reason not accessible in Russia). You can download the prepared CSV file with 2010 — 2019 data from here.
Unfortunately, no state population data exist for prior periods (2000 — 2009). We have therefore to narrow down our observation period to 9 years (from 2010 through 2018) for this part of the research.
POP_STATES_FILES = ROOT_FOLDER + '\\us_pop_states_race_2010-2019.csv'
df_pop_states = pd.read_csv(POP_STATES_FILES, sep=';', header=0)
# the source CSV has a specific format, so some trickery is required :)
df_pop_states = df_pop_states.melt('state_name', var_name='r_year', value_name='pop')
df_pop_states['race'] = df_pop_states['r_year'].str[0]
df_pop_states['year'] = df_pop_states['r_year'].str[2:].astype('uint16')
df_pop_states.drop(columns='r_year', inplace=True)
df_pop_states = df_pop_states[df_pop_states['year'].between(2000, 2018)]
df_pop_states = df_pop_states.groupby(['state_name', 'year', 'race']).sum().\
unstack().reset_index()
df_pop_states.columns = ['state_name', 'year', 'black_pop', 'white_pop']
White and Black population across states
SPL
year
black_pop
white_pop
state_name
Alabama
2010
5044936
13462236
Alabama
2011
5067912
13477008
Alabama
2012
5102512
13484256
Alabama
2013
5137360
13488812
Alabama
2014
5162316
13493432
...
...
...
...
Wyoming
2014
31392
2167008
Wyoming
2015
29568
2177740
Wyoming
2016
29304
2170700
Wyoming
2017
29444
2148128
Wyoming
2018
29604
2139896
Merging this data with the arrests dataset, we can calculate the per-million arrest counts:
df_arrests_2010_2018 = df_arrests.merge(df_pop_states, how='inner',
on=['year', 'state_name'])
df_arrests_2010_2018['white_arrests_promln'] = df_arrests_2010_2018['white'] * 1e6 /
df_arrests_2010_2018['white_pop']
df_arrests_2010_2018['black_arrests_promln'] = df_arrests_2010_2018['black'] * 1e6 /
df_arrests_2010_2018['black_pop']
And again let's calculate the year averages:
df_arrests_2010_2018_agg = df_arrests_2010_2018.groupby(
['state_name', 'state']).mean().drop(columns='year').reset_index()
df_arrests_2010_2018_agg = df_arrests_2010_2018_agg.set_index('state_name')
Combined arrest dataset with absolute and per-million counts
SPL
state
black
white
black_pop
white_pop
white_arrests_promln
black_arrests_promln
state_name
Alabama
AL
1682.000000
1342.000000
5.152399e+06
1.349158e+07
99.424741
324.055203
Alaska
AK
255.000000
870.555556
1.069489e+05
1.957445e+06
445.199704
2390.243876
Arizona
AZ
1635.555556
6852.000000
1.279172e+06
2.260403e+07
302.923002
1267.000192
Arkansas
AR
1960.666667
2466.000000
1.855574e+06
9.465137e+06
260.459917
1055.854934
California
CA
24381.666667
79477.000000
1.007921e+07
1.128020e+08
704.731408
2419.234376
Colorado
CO
1377.222222
5171.555556
9.508173e+05
1.882940e+07
274.209456
1439.257054
Connecticut
CT
1823.777778
2295.333333
1.643690e+06
1.165681e+07
196.712775
1114.811569
Delaware
DE
1318.000000
914.111111
8.354622e+05
2.635794e+06
347.374980
1582.395733
District of Columbia
DC
139.222222
4.777778
1.288488e+06
1.154416e+06
4.112547
108.101938
Florida
FL
12.000000
7.000000
1.415383e+07
6.498292e+07
0.107721
0.847827
Georgia
GA
8137.222222
4271.444444
1.279378e+07
2.500293e+07
170.939250
639.869143
Hawaii
HI
81.333333
383.777778
1.124298e+05
1.453712e+06
264.353469
725.477589
Idaho
ID
51.888889
1373.777778
5.288222e+04
6.154316e+06
223.151878
978.205026
Illinois
IL
4216.000000
1284.222222
7.554687e+06
3.980927e+07
32.199075
557.493894
Indiana
IN
2924.444444
5186.111111
2.522917e+06
2.267508e+07
228.699515
1155.168768
Iowa
IA
1181.000000
2999.222222
4.305640e+05
1.141794e+07
262.666753
2760.038539
Kansas
KS
539.555556
1512.111111
7.116182e+05
1.006714e+07
150.232160
758.851182
Kentucky
KY
1443.888889
2173.666667
1.442174e+06
1.558094e+07
139.526970
1001.433470
Louisiana
LA
5917.000000
3255.333333
6.021228e+06
1.174245e+07
277.277874
981.334817
Maine
ME
78.000000
678.000000
7.667733e+04
5.059062e+06
134.024032
1019.061684
Maryland
MD
6460.444444
3325.444444
7.229037e+06
1.426036e+07
233.317775
893.942720
Massachusetts
MA
3349.555556
6895.111111
2.249232e+06
2.226671e+07
309.745910
1505.096888
Michigan
MI
6302.444444
5647.444444
5.645176e+06
3.170670e+07
178.111684
1116.364030
Minnesota
MN
2570.000000
2686.777778
1.311818e+06
1.867259e+07
143.902882
1986.464052
Mississippi
MS
1251.000000
418.777778
4.478208e+06
7.122651e+06
58.753686
279.574565
Missouri
MO
4588.333333
5146.111111
2.854060e+06
2.023871e+07
254.292323
1608.303611
Montana
MT
34.222222
788.333333
2.210444e+04
3.660813e+06
214.944902
1525.795754
Nebraska
NE
618.888889
1154.888889
3.701520e+05
6.709768e+06
172.269972
1687.725359
Nevada
NV
2450.000000
4480.333333
1.052192e+06
8.647157e+06
517.401564
2316.374085
New Hampshire
NH
89.777778
784.777778
7.873600e+04
5.012056e+06
156.580888
1141.127571
New Jersey
NJ
5429.555556
4971.888889
5.241910e+06
2.595141e+07
191.427955
1037.217679
New Mexico
NM
260.111111
3136.000000
2.053876e+05
6.905377e+06
454.129135
1268.115549
New York
NY
6035.777778
6600.222222
1.373077e+07
5.534157e+07
119.253616
439.581451
North Carolina
NC
9549.000000
6759.333333
8.804027e+06
2.844145e+07
238.320077
1088.968561
North Dakota
ND
100.666667
386.222222
6.583289e+04
2.583206e+06
149.190455
1536.987272
Ohio
OH
3632.888889
3733.333333
5.879375e+06
3.844592e+07
97.107129
617.699379
Oklahoma
OK
1577.333333
3049.000000
1.189604e+06
1.160567e+07
262.904593
1326.463864
Oregon
OR
375.444444
3125.000000
3.292284e+05
1.402225e+07
222.819615
1148.158169
Pennsylvania
PA
11227.000000
10652.111111
5.945100e+06
4.232445e+07
251.598838
1893.415475
Rhode Island
RI
274.888889
595.000000
3.275551e+05
3.592825e+06
165.605635
837.932682
South Carolina
SC
4703.222222
3094.111111
5.365012e+06
1.324712e+07
234.287821
877.892998
South Dakota
SD
103.777778
448.333333
6.154533e+04
2.903489e+06
153.995184
1641.137012
Tennessee
TN
7603.000000
9068.666667
4.460808e+06
2.070126e+07
438.486812
1708.022356
Texas
TX
10821.666667
21122.111111
1.345661e+07
8.628389e+07
245.051258
803.917061
Utah
UT
193.222222
1797.333333
1.558876e+05
1.079659e+07
166.431266
1240.117890
Vermont
VT
54.222222
520.555556
3.017111e+04
2.376143e+06
219.129918
1785.111547
Virginia
VA
4059.555556
3071.222222
6.544598e+06
2.340732e+07
131.178648
620.504151
Washington
WA
1791.777778
5870.444444
1.147000e+06
2.289368e+07
256.632241
1566.862244
West Virginia
WV
294.111111
1648.666667
2.597649e+05
6.908718e+06
238.517207
1132.059057
Wisconsin
WI
3525.333333
4046.222222
1.516534e+06
2.018658e+07
200.441064
2325.622492
Wyoming
WY
28.777778
464.555556
2.856356e+04
2.151349e+06
216.004646
1005.725503
Let's visualize this stuff.
1. Absolute arrest counts
plt = df_arrests_2010_2018_agg[['white', 'black']].sort_index(ascending=False).\
plot.barh(color=['g', 'olive'], figsize=(10, 20))
plt.set_ylabel('')
plt.set_xlabel('Year-average arrest count (2010-2018)')
Tall image
SPL
2. Arrest counts per million population (for each race)
plt = df_arrests_2010_2018_agg[['white_arrests_promln', 'black_arrests_promln']].\
sort_index(ascending=False).plot.barh(color=['g', 'olive'], figsize=(10, 20))
plt.set_ylabel('')
plt.set_xlabel('Year-average arrest count per 1 mln. within race (2010-2018)')
Another tall image
SPL
What can we infer from this data?
First of all, we see that the number of arrests is affected by population — this is observed for both races.
Secondly, Whites get busted somewhat more often than Blacks in absolute figures. The 'somewhat' — because this rule isn't universal for all the states (exclusions are North Carolina, Georgia, Louisiana, etc.); at the same time, the difference is but slight in most states, except a few (like California, Texas, Colorado, Massachusetts and a few others).
Last but not least, Blacks get arrested much more often in all the states in per capita values.
Let's back these observations by numbers.
Difference between the average White and Black arrest counts:
df_arrests_2010_2018['white'].mean() / df_arrests_2010_2018['black'].mean()
— we get 1.56. That is, the observed 9 years saw on average one and a half times more Whites being arrested than Blacks.
Then in per capita values:
df_arrests_2010_2018['white_arrests_promln'].mean() /
df_arrests_2010_2018['black_arrests_promln'].mean()
— the ratio is 0.183. That is, a Black person is on average 5.5 times more likely to get arrested than a White person.
Thus, the previous conclusion of higher criminality among Blacks (compared to Whites) is confirmed by the arrest data for all the states of the USA.
To understand how race and criminality are connected with lethal force victims, let's merge the two datasets.
First, we prepare the use-of-force data with the victims' race details:
df_fenc_agg_states1 = df_fenc.merge(df_state_names, how='inner',
left_on='State', right_on='state_abbr')
df_fenc_agg_states1.fillna(0, inplace=True)
df_fenc_agg_states1 = df_fenc_agg_states1.rename(columns={
'state_name_x': 'state_name', 'Year': 'year'})
df_fenc_agg_states1 = df_fenc_agg_states1.loc[df_fenc_agg_states1['year'].\
between(2000, 2018), ['year', 'Race', 'state_name', 'UOF']]
df_fenc_agg_states1 = df_fenc_agg_states1.groupby(['year', 'state_name', 'Race'])['UOF'].\
count().unstack().reset_index()
df_fenc_agg_states1 = df_fenc_agg_states1.rename(columns={
'Black': 'black_uof', 'White': 'white_uof'})
df_fenc_agg_states1 = df_fenc_agg_states1.fillna(0).astype({
'black_uof': 'uint32', 'white_uof': 'uint32'})
Resulting UOF dataset
SPL
Race
year
state_name
black_uof
white_uof
0
2000
Alabama
4
3
1
2000
Alaska
0
2
2
2000
Arizona
0
11
3
2000
Arkansas
1
3
4
2000
California
19
78
...
...
...
...
...
907
2018
Virginia
11
7
908
2018
Washington
0
24
909
2018
West Virginia
2
5
910
2018
Wisconsin
3
7
911
2018
Wyoming
0
4
Then we're merging it with the arrest data:
df_arrests_fenc = df_arrests.merge(df_fenc_agg_states1,
on=['state_name', 'year'])
df_arrests_fenc = df_arrests_fenc.rename(columns={
'white': 'white_arrests', 'black': 'black_arrests'})
Example data for 2017
SPL
year
state
black_arrests
white_arrests
state_name
black_uof
white_uof
15
2017
AK
266
859
Alaska
2
3
34
2017
AL
3098
2509
Alabama
7
17
53
2017
AR
2092
2674
Arkansas
6
7
72
2017
AZ
2431
7829
Arizona
6
43
91
2017
CA
24937
80367
California
25
137
110
2017
CO
1781
6079
Colorado
2
27
127
2017
CT
1687
2114
Connecticut
1
5
140
2017
DE
1198
782
Delaware
4
3
159
2017
GA
7747
4171
Georgia
15
21
173
2017
HI
88
419
Hawaii
0
1
192
2017
IA
1400
3524
Iowa
1
5
210
2017
ID
61
1423
Idaho
0
6
229
2017
IL
2847
947
Illinois
13
11
248
2017
IN
3565
4300
Indiana
9
13
267
2017
KS
585
1651
Kansas
3
10
286
2017
KY
1481
2035
Kentucky
1
18
305
2017
LA
5875
2284
Louisiana
13
5
324
2017
MA
2953
6089
Massachusetts
1
4
343
2017
MD
6662
3371
Maryland
8
5
361
2017
ME
89
675
Maine
1
8
380
2017
MI
6149
5459
Michigan
6
7
399
2017
MN
2513
2681
Minnesota
1
7
418
2017
MO
4571
5007
Missouri
13
20
437
2017
MS
1266
409
Mississippi
7
10
455
2017
MT
50
915
Montana
0
3
474
2017
NC
8177
5576
North Carolina
9
14
501
2017
NE
80
578
Nebraska
0
1
516
2017
NH
113
817
New Hampshire
0
3
535
2017
NJ
4859
4136
New Jersey
9
6
554
2017
NM
205
2094
New Mexico
0
20
573
2017
NV
2695
4657
Nevada
3
12
592
2017
NY
5923
6633
New York
7
9
611
2017
OH
4472
3882
Ohio
11
23
630
2017
OK
1638
2872
Oklahoma
3
20
649
2017
OR
453
3222
Oregon
2
9
668
2017
PA
10123
10191
Pennsylvania
7
17
681
2017
RI
315
633
Rhode Island
0
1
700
2017
SC
4645
2964
South Carolina
3
10
712
2017
SD
124
537
South Dakota
0
2
731
2017
TN
6654
8496
Tennessee
4
24
750
2017
TX
11493
20911
Texas
18
56
769
2017
UT
199
1964
Utah
1
5
788
2017
VA
4283
3247
Virginia
8
17
804
2017
VT
75
626
Vermont
0
1
823
2017
WA
1890
5804
Washington
8
27
842
2017
WV
350
1705
West Virginia
1
10
856
2017
WY
36
549
Wyoming
0
1
872
2017
DC
135
8
District of Columbia
1
1
890
2017
WI
3604
4106
Wisconsin
6
15
892
2017
FL
12
7
Florida
19
43
OK, time to calculate the correlation coefficients between arrests and lethal force fatalities, as we did before:
df_corr = df_arrests_fenc.loc[:, ['white_arrests', 'black_arrests',
'white_uof', 'black_uof']].corr(method='pearson').iloc[:2, 2:]
df_corr.style.background_gradient(cmap='PuBu')
white_uof
black_uof
white_arrests
0.872766
0.622167
black_arrests
0.702350
0.766852
Again we've produced quite good correlations: 0.87 for Whites and 0.77 for Blacks. It's curious that these values are very close to those we obtained for All Offenses in the previous part of the article (0.88 for Whites and 0.72 for Blacks).
What about our 'offender shootdown' index? Let's check:
df_arrests_fenc['white_uof_by_arr'] = df_arrests_fenc['white_uof'] /
df_arrests_fenc['white_arrests']
df_arrests_fenc['black_uof_by_arr'] = df_arrests_fenc['black_uof'] /
df_arrests_fenc['black_arrests']
df_arrests_fenc.replace([np.inf, -np.inf], np.nan, inplace=True)
df_arrests_fenc.fillna({'white_uof_by_arr': 0, 'black_uof_by_arr': 0}, inplace=True)
To see how this index is distributed geographically, let's take the 2018 data point:
plt = df_arrests_fenc.loc[df_arrests_fenc['year'] == 2018,
['state_name', 'white_uof_by_arr', 'black_uof_by_arr']].\
sort_values(by='state_name', ascending=False).\
plot.barh(x='state_name', color=['g', 'olive'], figsize=(10, 20))
plt.set_ylabel('')
plt.set_xlabel('Ratio of UOF victims to violent crimes (2018)')
Tall image again
SPL
The index for Whites is greater in most states, with some exclusions (Utah, West Virginia, Kansas, Idaho, and District Columbia).
Let's compare the values for Whites and Blacks averaged for all the states:
plt = df_arrests_fenc.loc[:, ['white_uof_by_arr', 'black_uof_by_arr']].\
mean().plot.bar(color=['g', 'olive'])
plt.set_ylabel('Ratio of UOF victims to violent crimes (2018)')
plt.set_xticklabels(['White', 'Black'], rotation=0)

The index is 2.5 times greater for Whites than for Blacks. If this index really says something, it means that a White criminal is on average 2.5 times more likely to meet death from the police than a Black criminal. Of course, this index varies much from state to state: for example, in Idaho a Black criminal is twice as likely to become a law enforcement victim, whereas in Mississippi — four times less likely.
Well, that's it really. Time to summarize our research.
Conclusions
- In the US, criminality is a function of population. The most 'criminal' states that we are used to watching movies or read about are simply the most populated. When analyzing per capita crime rates, the top positions are taken by some quite unexpected states like Alaska, District Columbia (with Washington City) and New Mexico.
- Southern states are on average more criminal than Northern states (in per capita crime values).
- Per capita crimes and arrests are unevenly distributed among the US white and black populations: black persons commit 3 times more crimes and are 5 times more often arrested than white persons.
- A black person is on average 2.5 times more likely to get killed in an encounter with law enforcement than a white person.
- Lethal force fatalities correlate well with criminality: the higher the crime rate, the more people get killed by the police. This correlation holds true for most states and for both races, although it is somewhat more pronounced among the white population. This is also confirmed by the difference in the victim-to-crime ratio between the races: white criminals are more likely to get killed by the police.
As a final word, I'd like to say thanks to my readers for their valuable comments and advice.
P.S. In a future (separate) article I am planning to continue analyzing crime and its connection with race in the US. We can first look into hate crimes and then discuss the law enforcement / offender interfaces from a reversed point of view, investigating line-of-duty fatalities among US police officers. I'd appreciate if you let me know in the comments if this subject is of interest.
===========
Источник:
habr.com
===========
===========
Автор оригинала: S0mbre
===========Похожие новости:
- [GitHub, Open source, Расширения для браузеров, Софт] Разработка uMatrix закрыта
- [API, Big Data, Data Mining, Интерфейсы, Открытые данные] Парсинг сайта Умного Голосования и новый API на сайте ЦИК
- [*nix, Open source] FOSS News №34 – дайджест новостей свободного и открытого ПО за 14-20 сентября 2020 года
- [Финансы в IT] Хакеры остановили торги на бирже в Новой Зеландии
- [Python, Высокая производительность, Распределённые системы, Финансы в IT] Собираем данные AlphaVantage с Faust. Часть 1. Подготовка и введение
- [JavaScript, Node.JS] Подключение и настройка TradingView графиков
- [Python, Программирование, Визуальное программирование] Опыт проведения городской школьной олимпиады по программированию
- [Big Data, Искусственный интеллект, Машинное обучение] Временные сверточные сети – революция в мире временных рядов (перевод)
- [Google Cloud Platform, Python, R, Профессиональная литература] Учимся обращаться к данным и запрашивать их при помощи Google BigQuery. С примерами на Python и R (перевод)
- [GitHub, Go, Open source] Состоялся релиз консольной утилиты GitHub CLI 1.0
Теги для поиска: #_open_source, #_python, #_data_mining, #_big_data, #_python, #_pandas, #_api, #_rest, #_police, #_usa, #_statistics, #_big_data, #_black_lives_matter, #_open_source, #_open_source, #_python, #_data_mining, #_big_data
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 14-Янв 18:36
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 11 месяцев |
|
|
This is the concluding part of my article devoted to a statistical analysis of police shootings and criminality among the white and the black population of the United States. In the first part, we talked about the research background, goals, assumptions, and source data; in the second part, we investigated the national use-of-force and crime data and tracked their connection with race. Let's recall the intermediate inferences that we were able to make from the available data for 2000 — 2018:
Today, as I promised, we'll be looking at the geographical distribution of these data across the states, which ought to either confirm or confute the previous conclusions. However, before we take up geography, let's make a step back and see what happens if we analyze only the most violent offenses instead of 'All Offenses' as the source data for criminality. Many of my readers have pointed out in their comments that this would have been more proper, since 'All Offenses' incorporate those which should not (in practice) be associated with aggressive behavior provoking police shooting, such as petty larceny or selling drugs. I cannot whole-heartedly agree with this reasoning because, as I see it, any offense can arouse or heighten attention from the law enforcement, which in turn may wind up sadly… Still, let's just be curious enough to check! Assault and Murder Instead of All Offenses We just need to change one line of code where we form the crime dataset. Replace this line df_crimes1 = df_crimes1.loc[df_crimes1['Offense'] == 'All Offenses']
with this: df_crimes1 = df_crimes1.loc[df_crimes1['Offense'].str.contains('Assault|Murder')]
Our new filter now lets through only offenses connected with assault (simple and aggravated) and murder / non-negligent homicide (negligent / justifiable homicide / manslaughter cases are not included). We leave the rest of the code as it was. The number of crimes per 1 million population within each race now looks as follows:  We can see that, though the scale (Y-axis) is much lower, the shape of the curves is almost identical to the All Offenses ones we saw previously. The criminality vs. lethal force victims curves for both races:   And the correlation matrix: White_promln_cr White_promln_uof Black_promln_cr Black_promln_uof White_promln_cr 1.000000 0.684757 0.986622 0.729674 White_promln_uof 0.684757 1.000000 0.614132 0.795486 Black_promln_cr 0.986622 0.614132 1.000000 0.680893 Black_promln_uof 0.729674 0.795486 0.680893 1.000000 The correlation between criminality and lethal force fatalities is worse this time (0.68 against 0.88 and 0.72 for All Offenses). But the silver lining here is the fact that the correlation coefficients for Whites and Blacks are almost equal, which gives reason to say there is some constant correlation between crime and police shootings / victims (regardless of race). Now for our 'DIY' index — the ratio of lethal force deaths to the number of crimes (both per capita):  The difference here is even more apparent. The inference is the same: White criminals are more likely to get killed by the police than Black criminals. The summary is that all our prior conclusions hold true. Well, down to geography lessons now! :) Source Data To investigate criminality in individual states, I used different source endpoints in the FBI database:
Unfortunately, I didn't manage to get complete data on committed offenses with the offense state, year and offender race, much as I tried. The returned results had large gaps, for example, some states were totally omitted. But the alternative data on arrests is quite sufficient for our humble research. The first dataset contains crime counts for all the 51 states from 1991 to 2018, for the following offense categories:
For our purposes, we'll be using the 'violent crime' category, in keeping with the rest of the research. The second dataset features the number of arrests for the 51 states from 2000 to 2018, with details on the arrested persons' race (refer to the previous part for the race categories). Since the arrest dataset uses a different offense classification and doesn't provide the combined 'violent crime' category, the requests and retrieved results are for the four constituent offenses — murder / non-negligent manslaughter, robbery, rape, and aggravated assault. Crime Distribution (No Racial Factor) First, we'll look at the distribution of violent crimes across the states regardless of the offenders' race: import pandas as pd, numpy as np
CRIME_STATES_FILE = ROOT_FOLDER + '\\crimes_by_state.csv' df_crime_states = pd.read_csv(CRIME_STATES_FILE, sep=';', header=0, usecols=['year', 'state_abbr', 'population', 'violent_crime']) The resulting dataset: year state_abbr population violent_crime 0 2016 AL 4860545 25878 1 1996 AL 4273000 24159 2 1997 AL 4319000 24379 3 1998 AL 4352000 22286 4 1999 AL 4369862 21421 ... ... ... ... ... 1423 2000 DC 572059 8626 1424 2001 DC 573822 9195 1425 2002 DC 569157 9322 1426 2003 DC 557620 9061 1427 2016 DC 684336 8236 1428 rows × 4 columns Adding the full state names (the list of states we already used in our research — CSV) and optimizing / sorting the data: df_crime_states = df_crime_states.merge(df_state_names, on='state_abbr')
df_crime_states.dropna(inplace=True) df_crime_states.sort_values(by=['year', 'state_abbr'], inplace=True) Since the dataset already has population values, let's calculate the number of crimes per million people: df_crime_states['crime_promln'] = df_crime_states['violent_crime'] * 1e6 /
df_crime_states['population'] Finally, we'll turn the data into a table spanning the 2000 — 2018 period transposing the state names and dropping the redundant columns: df_crime_states_agg = df_crime_states.groupby(['state_name',
'year'])['violent_crime'].sum().unstack(level=1).T df_crime_states_agg.fillna(0, inplace=True) df_crime_states_agg = df_crime_states_agg.astype('uint32').loc[2000:2018, :] The resulting table contains 19 rows (year observations from 2000 through 2018) and 51 columns (by the number of states). Let's display the top 10 states for the average number of crimes: df_crime_states_agg_top10 = df_crime_states_agg.describe().T.nlargest(10, 'mean').\
astype('uint32') count mean std min 25% 50% 75% max state_name California 19 181514 19425 153763 165508 178597 193022 212867 Texas 19 117614 6522 104734 113212 121091 122084 126018 Florida 19 110104 18542 81980 92809 113541 127488 131878 New York 19 81618 9548 68495 75549 77563 85376 105111 Illinois 19 62866 10445 47775 54039 64185 69937 81196 Michigan 19 49273 5029 41712 44900 49737 54035 56981 Pennsylvania 19 46941 5066 39192 41607 48188 51021 55028 Tennessee 19 41951 2432 38063 40321 41562 43358 46482 Georgia 19 40228 3327 34355 38283 39435 41495 47353 North Carolina 19 37936 3193 32718 34706 38243 40258 43125 We'll also make it more graphic with a box plot: df_crime_states_top10 = df_crime_states_agg.loc[:, df_crime_states_agg_top10.index]
plt = df_crime_states_top10.plot.box(figsize=(12, 10)) plt.set_ylabel('Violent crime count (2000 - 2018)')  The 'Hollywood' state easily and notoriously beats the rest 9. The 'prizewinners' are California, Texas and Florida, all three in the South, the regular settings for most Hollywood criminal blockbusters. You can also see that criminality has changed considerably over the observed period in some states (California, Florida and Illinois), whereas in others (like Georgia) it has remained almost constant. I tend to think the crime rates are in some way connected with population :) Let's see the top 10 states by population in 2018: df_crime_states_2018 = df_crime_states.loc[df_crime_states['year'] == 2018]
plt = df_crime_states_2018.nlargest(10, 'population').\ sort_values(by='population').plot.barh(x='state_name', y='population', legend=False, figsize=(10,5)) plt.set_xlabel('2018 Population') plt.set_ylabel('')  Same old mugs here :) Let's check the correlation between crimes and population: df_corr = df_crime_states[df_crime_states['year']>=2000].groupby(['state_name']).mean()
df_corr = df_corr.loc[:, ['population', 'violent_crime']] df_corr.corr(method='pearson').at['population', 'violent_crime'] The calculated Pearson correlation coefficient is 0.98. Q.E.D. But the per capita crime counts give a staringly different picture: plt = df_crime_states_2018.nlargest(10, 'crime_promln').\
sort_values(by='crime_promln').plot.barh(x='state_name', y='crime_promln', legend=False, figsize=(10,5)) plt.set_xlabel('Number of violent crimes per 1 mln. population (2018)') plt.set_ylabel('')  There's a pretty kettle of fish! The leaders by per capita crimes are the least populated states: District Columbia (with the US capital) and Alaska (both home to some 700+ thousand people as of 2018), as well as one medium-populated state — New Mexico, with 2 mln. people. Only one state from our previous toplist is featured here — Tennessee, which gives this state a less-than-desirable reputation. We will then display these results on the US map. To do this, we need the folium library: import folium
First, the 2018 absolute crime counts: FOLIUM_URL = 'https://raw.githubusercontent.com/python-visualization/folium/master/examples/data'
FOLIUM_US_MAP = f'{FOLIUM_URL}/us-states.json' m = folium.Map(location=[48, -102], zoom_start=3) folium.Choropleth( geo_data=FOLIUM_US_MAP, name='choropleth', data=df_crime_states_2018, columns=['state_abbr', 'violent_crime'], key_on='feature.id', fill_color='YlOrRd', fill_opacity=0.7, line_opacity=0.2, legend_name='Violent crimes in 2018', bins=df_crime_states_2018['violent_crime'].quantile( list(np.linspace(0.0, 1.0, 5))).to_list(), reset=True ).add_to(m) folium.LayerControl().add_to(m) m  The same in per capita values (per 1 million): m = folium.Map(location=[48, -102], zoom_start=3)
folium.Choropleth( geo_data=FOLIUM_US_MAP, name='choropleth', data=df_crime_states_2018, columns=['state_abbr', 'crime_promln'], key_on='feature.id', fill_color='YlOrRd', fill_opacity=0.7, line_opacity=0.2, legend_name='Violent crimes in 2018 (per 1 mln. population)', bins=df_crime_states_2018['crime_promln'].quantile( list(np.linspace(0.0, 1.0, 5))).to_list(), reset=True ).add_to(m) folium.LayerControl().add_to(m) m  In the first case, as we can see, crimes are more or less evenly distributed in the North to South direction. In the second case, it's mostly the Southern states plus DC and Alaska that make the trend. Lethal Force Fatalities Across States (No Racial Factor) We are now going to look at lethal force used in individual states across the country. To prepare the dataset, we'll complement the UOF (Use Of Force) data we used previously by the full state names, group the cases by states, and constrain the observations to years 2000 through 2018: df_fenc_agg_states = df_fenc.merge(df_state_names, how='inner',
left_on='State', right_on='state_abbr') df_fenc_agg_states.fillna(0, inplace=True) df_fenc_agg_states = df_fenc_agg_states.rename(columns={'state_name_x': 'State Name'}) df_fenc_agg_states = df_fenc_agg_states.loc[:, ['Year', 'Race', 'State', 'State Name', 'Cause', 'UOF']] df_fenc_agg_states = df_fenc_agg_states.\ groupby(['Year', 'State Name', 'State'])['UOF'].\ count().unstack(level=0) df_fenc_agg_states.fillna(0, inplace=True) df_fenc_agg_states = df_fenc_agg_states.astype('uint16').loc[:, :2018] df_fenc_agg_states = df_fenc_agg_states.reset_index() Top 10 states for police victims in 2018: df_fenc_agg_states_2018 = df_fenc_agg_states.loc[:, ['State Name', 2018]]
plt = df_fenc_agg_states_2018.nlargest(10, 2018).sort_values(2018).plot.barh( x='State Name', y=2018, legend=False, figsize=(10,5)) plt.set_xlabel('Number of UOF victims in 2018') plt.set_ylabel('')  Let's also review the data for the entire period as a box plot: fenc_top10 = df_fenc_agg_states.loc[df_fenc_agg_states['State Name'].\
isin(df_fenc_agg_states_2018.nlargest(10, 2018)['State Name'])] fenc_top10 = fenc_top10.T fenc_top10.columns = fenc_top10.loc['State Name', :] fenc_top10 = fenc_top10.reset_index().loc[2:, :].set_index('Year') df_sorted = fenc_top10.mean().sort_values(ascending=False) fenc_top10 = fenc_top10.loc[:, df_sorted.index] plt = fenc_top10.plot.box(figsize=(12, 6)) plt.set_ylabel('Number of UOF victims (2000 - 2018)')  Yep! The same 'unholy trio' of California, Texas and Florida, with their other two Southern sidekicks — Arizona and Georgia. The leaders again show large scatter indicative of year-to-year changes. Connection Between Lethal Force Fatalities and Crimes As in the previous part of this research, we are investigating the possible connection between criminality and deaths at the hands of law enforcement. We'll start without the racial factor, to see if such a connection exists in principle and how it varies from state to state. At first, we must merge the UOF and (violent) crime datasets, setting the observation period to 2000 — 2018: # add full state names
df_fenc_crime_states = df_fenc.merge(df_state_names, how='inner', left_on='State', right_on='state_abbr') # rename some columns df_fenc_crime_states = df_fenc_crime_states.rename(columns={'Year': 'year', 'state_name_x': 'state_name'}) # truncate period to 2000-2018 df_fenc_crime_states = df_fenc_crime_states[df_fenc_crime_states['year'].between(2000, 2018)] # group by year and state df_fenc_crime_states = df_fenc_crime_states.groupby(['year', 'state_name'])['UOF'].\ count().reset_index() # join with crime data df_fenc_crime_states = df_fenc_crime_states.merge(df_crime_states[df_crime_states['year'].\ between(2000, 2018)], how='outer', on=['year', 'state_name']) # set missing data to zero df_fenc_crime_states.fillna({'UOF': 0}, inplace=True) # unify data types df_fenc_crime_states = df_fenc_crime_states.astype({'year': 'uint16', 'UOF': 'uint16', 'population': 'uint32', 'violent_crime': 'uint32'}) # sort data df_fenc_crime_states = df_fenc_crime_states.sort_values(by=['year', 'state_name']) Resulting datasetSPLyear state_name UOF state_abbr population violent_crime crime_promln 0 2000 Alabama 7 AL 4447100 21620 4861.595197 1 2000 Alaska 2 AK 626932 3554 5668.876369 2 2000 Arizona 11 AZ 5130632 27281 5317.278651 3 2000 Arkansas 4 AR 2673400 11904 4452.756789 4 2000 California 97 CA 33871648 210531 6215.552311 ... ... ... ... ... ... ... ... 907 2018 Virginia 18 VA 8517685 17032 1999.604353 908 2018 Washington 24 WA 7535591 23472 3114.818732 909 2018 West Virginia 7 WV 1805832 5236 2899.494527 910 2018 Wisconsin 10 WI 5813568 17176 2954.467893 911 2018 Wyoming 4 WY 577737 1226 2122.072846 As you will remember, the UOF column contains the number of deaths from encounters with law enforcement officers (who I sometimes call here just 'the police', but who include, of course, other agencies such as the FBI) where lethal force was used intentionally. We will also make a separate dataset with year-average values: df_fenc_crime_states_agg = df_fenc_crime_states.groupby(['state_name']).\
mean().loc[:, ['UOF', 'violent_crime']] Now let's look at the year averages for crimes and lethal force fatalities for all the 51 states on one plot: plt = df_fenc_crime_states_agg['violent_crime'].plot.bar(legend=True, figsize=(15,5))
plt.set_ylabel('Number of violent crimes (year average)') plt2 = df_fenc_crime_states_agg['UOF'].plot(secondary_y=True, style='g', legend=True) plt2.set_ylabel('Number of UOF victims (year average)', rotation=90) plt2.set_xlabel('') plt.set_xlabel('') plt.set_xticklabels(df_fenc_crime_states_agg.index, rotation='vertical')  Looking closely at this combined chart, one can see the following:
Let's also make a scatterplot: plt = df_fenc_crime_states_agg.plot.scatter(x='violent_crime', y='UOF')
plt.set_xlabel('Number of violent crimes (year average)') plt.set_ylabel('Number of UOF victims (year average)')  Here it becomes conspicuous that the ratio between crime and use of lethal force is affected by the crime rate. Speaking crudely, in states with the number of violent crimes below 75k the number of police victims grows more slowly; whereas in the states with the crime count above 75k this growth is quite steep. This latter group includes, as we can see, only four states. Let's look them 'in the face': df_fenc_crime_states_agg[df_fenc_crime_states_agg['violent_crime'] > 75000]
UOF violent_crime state_name California 133.263158 181514.578947 Florida 54.578947 110104.315789 New York 19.157895 81618.052632 Texas 64.368421 117614.631579 Will you be surprised? We've got the same 'four horsemen of the Apocalypse': California, Florida, Texas and New York. Correspondingly, let's calculate the correlation coefficients between our data for three cases:
For the first case: df_fenc_crime_states_agg[df_fenc_crime_states_agg['violent_crime'] <= \
75000].corr(method='pearson').at['UOF', 'violent_crime'] — we obtain 0.839 as the correlation coefficient. This is a statistically valid value, although it doesn't reach 0.9 due to scatter across the 47 states. For the first case: df_fenc_crime_states_agg[df_fenc_crime_states_agg['violent_crime'] > \
75000].corr(method='pearson').at['UOF', 'violent_crime'] — we get 0.999 — an ideal correlation! For the last case (all states): df_fenc_crime_states_agg.corr(method='pearson').at['UOF', 'violent_crime']
— the correlation is estimated at 0.935. This overall correlation may be considered very good. Let's now look at the geographical distribution of our 'offender shootdown' index (the term is coined here for brevity). As before, we divide the number of lethal force fatalities by the number of crimes: df_fenc_crime_states_agg['uof_by_crime'] = df_fenc_crime_states_agg['UOF'] /
df_fenc_crime_states_agg['violent_crime'] plt = df_fenc_crime_states_agg.loc[:, 'uof_by_crime'].sort_values(ascending=False).\ plot.bar(figsize=(15,5)) plt.set_xlabel('') plt.set_ylabel('Ratio of UOF victims to number of violent crimes')  It is interesting to observe that our erstwhile leaders have shifted toward the center or even the rightmost end of the chart, which must mean that the most criminal states don't have the most 'bloodthirsty' police (towards real or potential offenders). Intermediate conclusions:
Racial Factor in Criminality and Lethal Force Fatalities Across States Proving that crime rates do affect police victim rates, let's add the racial factor and see what it affects. As I explained above, we'll be using the arrest data for this purpose as being the most complete and covering the main offenses for all the states. There is, of course, no such state or country where one could equate the number of committed crimes to the number of arrests; yet these parameters are closely related. As such, we can do very well with arrest data for our statistical analysis. And, as we already agreed, only violent offenses (murder, rape, robbery, aggravated assault) will be taken into account. Let's load the source data from the CSV file and routinely add the full state names: ARRESTS_FILE = ROOT_FOLDER + '\\arrests_by_state_race.csv'
# arrests of Blacks and Whites only df_arrests = pd.read_csv(ARRESTS_FILE, sep=';', header=0, usecols=['data_year', 'state', 'white', 'black']) # sum the four offenses and group by states df_arrests = df_arrests.groupby(['data_year', 'state']).sum().reset_index() # add state names df_arrests = df_arrests.merge(df_state_names, left_on='state', right_on='state_abbr') # rename / remove columns df_arrests = df_arrests.rename(columns={'data_year': 'year'}).drop(columns='state_abbr') # peek at the result df_arrests.head() year state black white state_name 0 2000 AK 140 613 Alaska 1 2001 AK 139 718 Alaska 2 2002 AK 143 677 Alaska 3 2003 AK 173 801 Alaska 4 2004 AK 163 765 Alaska We'll also create a dataframe with year average values: df_arrests_agg = df_arrests.groupby(['state_name']).mean().drop(columns='year')
Arrests of Whites and Blacks in 51 states (year average counts)SPLblack white state_name Alabama 2805.842105 1757.315789 Alaska 221.894737 844.157895 Arizona 1378.368421 7007.157895 Arkansas 2387.894737 2303.789474 California 26668.368421 87252.315789 Colorado 1268.210526 5157.368421 Connecticut 2097.631579 2981.210526 Delaware 1356.894737 1048.578947 District of Columbia 111.111111 4.944444 Florida 12.000000 7.000000 Georgia 8262.842105 3502.894737 Hawaii 81.052632 368.736842 Idaho 44.000000 1362.263158 Illinois 5699.842105 1841.894737 Indiana 3553.368421 5192.263158 Iowa 1104.421053 3039.473684 Kansas 522.315789 1501.315789 Kentucky 1476.894737 1906.052632 Louisiana 5928.789474 3414.263158 Maine 63.736842 699.526316 Maryland 7189.105263 4010.684211 Massachusetts 3407.157895 7319.684211 Michigan 7628.157895 6304.157895 Minnesota 2231.210526 2645.736842 Mississippi 1462.210526 474.368421 Missouri 5777.473684 5703.368421 Montana 27.684211 673.684211 Nebraska 591.421053 1058.526316 Nevada 1956.421053 3817.210526 New Hampshire 68.368421 640.789474 New Jersey 6424.157895 6043.789474 New Mexico 234.421053 2809.368421 New York 8394.526316 8734.947368 North Carolina 10527.947368 7412.947368 North Dakota 61.263158 277.052632 Ohio 4063.947368 4071.368421 Oklahoma 1625.105263 3353.000000 Oregon 445.105263 3373.368421 Pennsylvania 11974.157895 11039.473684 Rhode Island 275.684211 699.210526 South Carolina 5578.526316 3615.421053 South Dakota 67.105263 349.368421 Tennessee 6799.894737 8462.526316 Texas 10547.631579 22062.684211 Utah 167.105263 1748.894737 Vermont 43.526316 439.210526 Virginia 4100.421053 3060.263158 Washington 1688.947368 6012.105263 West Virginia 271.263158 1528.315789 Wisconsin 3440.055556 4107.722222 Wyoming 27.263158 506.947368 Looking at this table, one can't overlook some oddities. In some states the arrest counts reach hundreds and thousands, while in others — only dozens or fewer. That's the case with Florida, one of the most populated states: it counts only 19 arrests per year (12 Blacks and 7 Whites). Surely, some data is missing here; let's check: df_arrests[df_arrests['state'] == 'FL']
And indeed we see that data for Florida is available only for 2017. Well, we'll have to put up with this, I suppose. All the other states have complete data. But the ten / hundred-fold difference should be accounted for by population. Let's add population-by-race data and have a look. The population data was taken from the US Census Bureau website (which is for some reason not accessible in Russia). You can download the prepared CSV file with 2010 — 2019 data from here. Unfortunately, no state population data exist for prior periods (2000 — 2009). We have therefore to narrow down our observation period to 9 years (from 2010 through 2018) for this part of the research. POP_STATES_FILES = ROOT_FOLDER + '\\us_pop_states_race_2010-2019.csv'
df_pop_states = pd.read_csv(POP_STATES_FILES, sep=';', header=0) # the source CSV has a specific format, so some trickery is required :) df_pop_states = df_pop_states.melt('state_name', var_name='r_year', value_name='pop') df_pop_states['race'] = df_pop_states['r_year'].str[0] df_pop_states['year'] = df_pop_states['r_year'].str[2:].astype('uint16') df_pop_states.drop(columns='r_year', inplace=True) df_pop_states = df_pop_states[df_pop_states['year'].between(2000, 2018)] df_pop_states = df_pop_states.groupby(['state_name', 'year', 'race']).sum().\ unstack().reset_index() df_pop_states.columns = ['state_name', 'year', 'black_pop', 'white_pop'] White and Black population across statesSPLyear black_pop white_pop state_name Alabama 2010 5044936 13462236 Alabama 2011 5067912 13477008 Alabama 2012 5102512 13484256 Alabama 2013 5137360 13488812 Alabama 2014 5162316 13493432 ... ... ... ... Wyoming 2014 31392 2167008 Wyoming 2015 29568 2177740 Wyoming 2016 29304 2170700 Wyoming 2017 29444 2148128 Wyoming 2018 29604 2139896 Merging this data with the arrests dataset, we can calculate the per-million arrest counts: df_arrests_2010_2018 = df_arrests.merge(df_pop_states, how='inner',
on=['year', 'state_name']) df_arrests_2010_2018['white_arrests_promln'] = df_arrests_2010_2018['white'] * 1e6 / df_arrests_2010_2018['white_pop'] df_arrests_2010_2018['black_arrests_promln'] = df_arrests_2010_2018['black'] * 1e6 / df_arrests_2010_2018['black_pop'] And again let's calculate the year averages: df_arrests_2010_2018_agg = df_arrests_2010_2018.groupby(
['state_name', 'state']).mean().drop(columns='year').reset_index() df_arrests_2010_2018_agg = df_arrests_2010_2018_agg.set_index('state_name') Combined arrest dataset with absolute and per-million countsSPLstate black white black_pop white_pop white_arrests_promln black_arrests_promln state_name Alabama AL 1682.000000 1342.000000 5.152399e+06 1.349158e+07 99.424741 324.055203 Alaska AK 255.000000 870.555556 1.069489e+05 1.957445e+06 445.199704 2390.243876 Arizona AZ 1635.555556 6852.000000 1.279172e+06 2.260403e+07 302.923002 1267.000192 Arkansas AR 1960.666667 2466.000000 1.855574e+06 9.465137e+06 260.459917 1055.854934 California CA 24381.666667 79477.000000 1.007921e+07 1.128020e+08 704.731408 2419.234376 Colorado CO 1377.222222 5171.555556 9.508173e+05 1.882940e+07 274.209456 1439.257054 Connecticut CT 1823.777778 2295.333333 1.643690e+06 1.165681e+07 196.712775 1114.811569 Delaware DE 1318.000000 914.111111 8.354622e+05 2.635794e+06 347.374980 1582.395733 District of Columbia DC 139.222222 4.777778 1.288488e+06 1.154416e+06 4.112547 108.101938 Florida FL 12.000000 7.000000 1.415383e+07 6.498292e+07 0.107721 0.847827 Georgia GA 8137.222222 4271.444444 1.279378e+07 2.500293e+07 170.939250 639.869143 Hawaii HI 81.333333 383.777778 1.124298e+05 1.453712e+06 264.353469 725.477589 Idaho ID 51.888889 1373.777778 5.288222e+04 6.154316e+06 223.151878 978.205026 Illinois IL 4216.000000 1284.222222 7.554687e+06 3.980927e+07 32.199075 557.493894 Indiana IN 2924.444444 5186.111111 2.522917e+06 2.267508e+07 228.699515 1155.168768 Iowa IA 1181.000000 2999.222222 4.305640e+05 1.141794e+07 262.666753 2760.038539 Kansas KS 539.555556 1512.111111 7.116182e+05 1.006714e+07 150.232160 758.851182 Kentucky KY 1443.888889 2173.666667 1.442174e+06 1.558094e+07 139.526970 1001.433470 Louisiana LA 5917.000000 3255.333333 6.021228e+06 1.174245e+07 277.277874 981.334817 Maine ME 78.000000 678.000000 7.667733e+04 5.059062e+06 134.024032 1019.061684 Maryland MD 6460.444444 3325.444444 7.229037e+06 1.426036e+07 233.317775 893.942720 Massachusetts MA 3349.555556 6895.111111 2.249232e+06 2.226671e+07 309.745910 1505.096888 Michigan MI 6302.444444 5647.444444 5.645176e+06 3.170670e+07 178.111684 1116.364030 Minnesota MN 2570.000000 2686.777778 1.311818e+06 1.867259e+07 143.902882 1986.464052 Mississippi MS 1251.000000 418.777778 4.478208e+06 7.122651e+06 58.753686 279.574565 Missouri MO 4588.333333 5146.111111 2.854060e+06 2.023871e+07 254.292323 1608.303611 Montana MT 34.222222 788.333333 2.210444e+04 3.660813e+06 214.944902 1525.795754 Nebraska NE 618.888889 1154.888889 3.701520e+05 6.709768e+06 172.269972 1687.725359 Nevada NV 2450.000000 4480.333333 1.052192e+06 8.647157e+06 517.401564 2316.374085 New Hampshire NH 89.777778 784.777778 7.873600e+04 5.012056e+06 156.580888 1141.127571 New Jersey NJ 5429.555556 4971.888889 5.241910e+06 2.595141e+07 191.427955 1037.217679 New Mexico NM 260.111111 3136.000000 2.053876e+05 6.905377e+06 454.129135 1268.115549 New York NY 6035.777778 6600.222222 1.373077e+07 5.534157e+07 119.253616 439.581451 North Carolina NC 9549.000000 6759.333333 8.804027e+06 2.844145e+07 238.320077 1088.968561 North Dakota ND 100.666667 386.222222 6.583289e+04 2.583206e+06 149.190455 1536.987272 Ohio OH 3632.888889 3733.333333 5.879375e+06 3.844592e+07 97.107129 617.699379 Oklahoma OK 1577.333333 3049.000000 1.189604e+06 1.160567e+07 262.904593 1326.463864 Oregon OR 375.444444 3125.000000 3.292284e+05 1.402225e+07 222.819615 1148.158169 Pennsylvania PA 11227.000000 10652.111111 5.945100e+06 4.232445e+07 251.598838 1893.415475 Rhode Island RI 274.888889 595.000000 3.275551e+05 3.592825e+06 165.605635 837.932682 South Carolina SC 4703.222222 3094.111111 5.365012e+06 1.324712e+07 234.287821 877.892998 South Dakota SD 103.777778 448.333333 6.154533e+04 2.903489e+06 153.995184 1641.137012 Tennessee TN 7603.000000 9068.666667 4.460808e+06 2.070126e+07 438.486812 1708.022356 Texas TX 10821.666667 21122.111111 1.345661e+07 8.628389e+07 245.051258 803.917061 Utah UT 193.222222 1797.333333 1.558876e+05 1.079659e+07 166.431266 1240.117890 Vermont VT 54.222222 520.555556 3.017111e+04 2.376143e+06 219.129918 1785.111547 Virginia VA 4059.555556 3071.222222 6.544598e+06 2.340732e+07 131.178648 620.504151 Washington WA 1791.777778 5870.444444 1.147000e+06 2.289368e+07 256.632241 1566.862244 West Virginia WV 294.111111 1648.666667 2.597649e+05 6.908718e+06 238.517207 1132.059057 Wisconsin WI 3525.333333 4046.222222 1.516534e+06 2.018658e+07 200.441064 2325.622492 Wyoming WY 28.777778 464.555556 2.856356e+04 2.151349e+06 216.004646 1005.725503 Let's visualize this stuff. 1. Absolute arrest counts plt = df_arrests_2010_2018_agg[['white', 'black']].sort_index(ascending=False).\
plot.barh(color=['g', 'olive'], figsize=(10, 20)) plt.set_ylabel('') plt.set_xlabel('Year-average arrest count (2010-2018)') Tall imageSPL2. Arrest counts per million population (for each race) plt = df_arrests_2010_2018_agg[['white_arrests_promln', 'black_arrests_promln']].\
sort_index(ascending=False).plot.barh(color=['g', 'olive'], figsize=(10, 20)) plt.set_ylabel('') plt.set_xlabel('Year-average arrest count per 1 mln. within race (2010-2018)') Another tall imageSPLWhat can we infer from this data? First of all, we see that the number of arrests is affected by population — this is observed for both races. Secondly, Whites get busted somewhat more often than Blacks in absolute figures. The 'somewhat' — because this rule isn't universal for all the states (exclusions are North Carolina, Georgia, Louisiana, etc.); at the same time, the difference is but slight in most states, except a few (like California, Texas, Colorado, Massachusetts and a few others). Last but not least, Blacks get arrested much more often in all the states in per capita values. Let's back these observations by numbers. Difference between the average White and Black arrest counts: df_arrests_2010_2018['white'].mean() / df_arrests_2010_2018['black'].mean()
— we get 1.56. That is, the observed 9 years saw on average one and a half times more Whites being arrested than Blacks. Then in per capita values: df_arrests_2010_2018['white_arrests_promln'].mean() /
df_arrests_2010_2018['black_arrests_promln'].mean() — the ratio is 0.183. That is, a Black person is on average 5.5 times more likely to get arrested than a White person. Thus, the previous conclusion of higher criminality among Blacks (compared to Whites) is confirmed by the arrest data for all the states of the USA. To understand how race and criminality are connected with lethal force victims, let's merge the two datasets. First, we prepare the use-of-force data with the victims' race details: df_fenc_agg_states1 = df_fenc.merge(df_state_names, how='inner',
left_on='State', right_on='state_abbr') df_fenc_agg_states1.fillna(0, inplace=True) df_fenc_agg_states1 = df_fenc_agg_states1.rename(columns={ 'state_name_x': 'state_name', 'Year': 'year'}) df_fenc_agg_states1 = df_fenc_agg_states1.loc[df_fenc_agg_states1['year'].\ between(2000, 2018), ['year', 'Race', 'state_name', 'UOF']] df_fenc_agg_states1 = df_fenc_agg_states1.groupby(['year', 'state_name', 'Race'])['UOF'].\ count().unstack().reset_index() df_fenc_agg_states1 = df_fenc_agg_states1.rename(columns={ 'Black': 'black_uof', 'White': 'white_uof'}) df_fenc_agg_states1 = df_fenc_agg_states1.fillna(0).astype({ 'black_uof': 'uint32', 'white_uof': 'uint32'}) Resulting UOF datasetSPLRace year state_name black_uof white_uof 0 2000 Alabama 4 3 1 2000 Alaska 0 2 2 2000 Arizona 0 11 3 2000 Arkansas 1 3 4 2000 California 19 78 ... ... ... ... ... 907 2018 Virginia 11 7 908 2018 Washington 0 24 909 2018 West Virginia 2 5 910 2018 Wisconsin 3 7 911 2018 Wyoming 0 4 Then we're merging it with the arrest data: df_arrests_fenc = df_arrests.merge(df_fenc_agg_states1,
on=['state_name', 'year']) df_arrests_fenc = df_arrests_fenc.rename(columns={ 'white': 'white_arrests', 'black': 'black_arrests'}) Example data for 2017SPLyear state black_arrests white_arrests state_name black_uof white_uof 15 2017 AK 266 859 Alaska 2 3 34 2017 AL 3098 2509 Alabama 7 17 53 2017 AR 2092 2674 Arkansas 6 7 72 2017 AZ 2431 7829 Arizona 6 43 91 2017 CA 24937 80367 California 25 137 110 2017 CO 1781 6079 Colorado 2 27 127 2017 CT 1687 2114 Connecticut 1 5 140 2017 DE 1198 782 Delaware 4 3 159 2017 GA 7747 4171 Georgia 15 21 173 2017 HI 88 419 Hawaii 0 1 192 2017 IA 1400 3524 Iowa 1 5 210 2017 ID 61 1423 Idaho 0 6 229 2017 IL 2847 947 Illinois 13 11 248 2017 IN 3565 4300 Indiana 9 13 267 2017 KS 585 1651 Kansas 3 10 286 2017 KY 1481 2035 Kentucky 1 18 305 2017 LA 5875 2284 Louisiana 13 5 324 2017 MA 2953 6089 Massachusetts 1 4 343 2017 MD 6662 3371 Maryland 8 5 361 2017 ME 89 675 Maine 1 8 380 2017 MI 6149 5459 Michigan 6 7 399 2017 MN 2513 2681 Minnesota 1 7 418 2017 MO 4571 5007 Missouri 13 20 437 2017 MS 1266 409 Mississippi 7 10 455 2017 MT 50 915 Montana 0 3 474 2017 NC 8177 5576 North Carolina 9 14 501 2017 NE 80 578 Nebraska 0 1 516 2017 NH 113 817 New Hampshire 0 3 535 2017 NJ 4859 4136 New Jersey 9 6 554 2017 NM 205 2094 New Mexico 0 20 573 2017 NV 2695 4657 Nevada 3 12 592 2017 NY 5923 6633 New York 7 9 611 2017 OH 4472 3882 Ohio 11 23 630 2017 OK 1638 2872 Oklahoma 3 20 649 2017 OR 453 3222 Oregon 2 9 668 2017 PA 10123 10191 Pennsylvania 7 17 681 2017 RI 315 633 Rhode Island 0 1 700 2017 SC 4645 2964 South Carolina 3 10 712 2017 SD 124 537 South Dakota 0 2 731 2017 TN 6654 8496 Tennessee 4 24 750 2017 TX 11493 20911 Texas 18 56 769 2017 UT 199 1964 Utah 1 5 788 2017 VA 4283 3247 Virginia 8 17 804 2017 VT 75 626 Vermont 0 1 823 2017 WA 1890 5804 Washington 8 27 842 2017 WV 350 1705 West Virginia 1 10 856 2017 WY 36 549 Wyoming 0 1 872 2017 DC 135 8 District of Columbia 1 1 890 2017 WI 3604 4106 Wisconsin 6 15 892 2017 FL 12 7 Florida 19 43 OK, time to calculate the correlation coefficients between arrests and lethal force fatalities, as we did before: df_corr = df_arrests_fenc.loc[:, ['white_arrests', 'black_arrests',
'white_uof', 'black_uof']].corr(method='pearson').iloc[:2, 2:] df_corr.style.background_gradient(cmap='PuBu') white_uof black_uof white_arrests 0.872766 0.622167 black_arrests 0.702350 0.766852 Again we've produced quite good correlations: 0.87 for Whites and 0.77 for Blacks. It's curious that these values are very close to those we obtained for All Offenses in the previous part of the article (0.88 for Whites and 0.72 for Blacks). What about our 'offender shootdown' index? Let's check: df_arrests_fenc['white_uof_by_arr'] = df_arrests_fenc['white_uof'] /
df_arrests_fenc['white_arrests'] df_arrests_fenc['black_uof_by_arr'] = df_arrests_fenc['black_uof'] / df_arrests_fenc['black_arrests'] df_arrests_fenc.replace([np.inf, -np.inf], np.nan, inplace=True) df_arrests_fenc.fillna({'white_uof_by_arr': 0, 'black_uof_by_arr': 0}, inplace=True) To see how this index is distributed geographically, let's take the 2018 data point: plt = df_arrests_fenc.loc[df_arrests_fenc['year'] == 2018,
['state_name', 'white_uof_by_arr', 'black_uof_by_arr']].\ sort_values(by='state_name', ascending=False).\ plot.barh(x='state_name', color=['g', 'olive'], figsize=(10, 20)) plt.set_ylabel('') plt.set_xlabel('Ratio of UOF victims to violent crimes (2018)') Tall image againSPLThe index for Whites is greater in most states, with some exclusions (Utah, West Virginia, Kansas, Idaho, and District Columbia). Let's compare the values for Whites and Blacks averaged for all the states: plt = df_arrests_fenc.loc[:, ['white_uof_by_arr', 'black_uof_by_arr']].\
mean().plot.bar(color=['g', 'olive']) plt.set_ylabel('Ratio of UOF victims to violent crimes (2018)') plt.set_xticklabels(['White', 'Black'], rotation=0)  The index is 2.5 times greater for Whites than for Blacks. If this index really says something, it means that a White criminal is on average 2.5 times more likely to meet death from the police than a Black criminal. Of course, this index varies much from state to state: for example, in Idaho a Black criminal is twice as likely to become a law enforcement victim, whereas in Mississippi — four times less likely. Well, that's it really. Time to summarize our research. Conclusions
As a final word, I'd like to say thanks to my readers for their valuable comments and advice. P.S. In a future (separate) article I am planning to continue analyzing crime and its connection with race in the US. We can first look into hate crimes and then discuss the law enforcement / offender interfaces from a reversed point of view, investigating line-of-duty fatalities among US police officers. I'd appreciate if you let me know in the comments if this subject is of interest. =========== Источник: habr.com =========== =========== Автор оригинала: S0mbre ===========Похожие новости:
|
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 14-Янв 18:36
Часовой пояс: UTC + 5



