[Python, Программирование] Напишем и поймем Decision Tree на Python с нуля! Часть 1. Краткий обзор (перевод)
Автор
Сообщение
news_bot ®
Стаж: 8 лет
Сообщений: 27286
Привет, Хабр! Представляю вашему вниманию перевод статьи "Pythonで0からディシジョンツリーを作って理解する (1. 概要編)".
1.1 Что такое Decision Tree?
1.1.1 Пример Decision Tree
Например, у нас есть следующий набор данных (дата сет): погода, температура, влажность, ветер, игра в гольф. В зависимости от погоды и остального, мы ходили (〇) или не ходили (×) играть в гольф. Предположим, что у нас есть 14 сложившихся вариантов.

Из этих данных мы можем составить структуру данных, показывающую, в каких случаях мы шли на гольф. Такая структура из-за своей ветвистой формы называется Decision Tree.
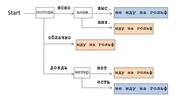
Например, если посмотреть на Decision Tree, изображенный на картинке выше, мы поймем, что сначала проверяли погоду. Если было ясно, мы проверяли влажность: если она высокая, то не шли играть в гольф, если низкая — шли. А если погода была облачная, то шли играть в гольф вне зависимости от других условий.
1.1.2 Об этой статье
Существуют алгоритмы, которые создают такие Decision Tree автоматически, на основе имеющихся данных. В этой статье мы будем использовать алгоритм ID3 на Python.
Эта статья — первая из серии. Следующие статьи:
(Прим. переводчика: “если вас заинтересует продолжение, пожалуйста, сообщите нам в в комментариях”.)
・Основы программирования на Python
・Необходимые основы библиотеки для анализа данных Pandas
・Основы структуры данных (в случае с Decision Tree)
・Основы информационной энтропии
・Учим алгоритм для генерации Decision Tree
1.1.3 Немного о Decision Tree
Генерация Decision Tree связана с машинным обучением с учителем и классификацией. Классификация в машинном обучении — способ, позволяющий создать модель, ведущую к правильному ответу, на основе обучении на дата сете с правильными ответами и ведущими к ним данными. Глубокое обучение (Deep Learning), которое в последние годы очень популярно, особенно в сфере распознавания изображений, тоже является частью машинного обучения на основе классификационного метода. Разница Deep Learning и Decision Tree в том, приводится ли конечный результат к форме, при которой человек понимает принципы генерации конечной структуры данных. Особенность Deep Learning — мы получаем конечный результат, но не понимаем принцип его генерации. В отличие от Deep Learning, принцип построения Decision Tree прост для понимания человеком, что также является его важной особенностью.
Эта особенность Decision Tree хороша не только для машинного обучения, но и дата майнинга, где также важно понимание данных пользователем.
1.2 Об алгоритме ID3
ID3 — алгоритм генерации Decision Tree, разработанный в 1986 году Россом Куинланом. У него есть две важные особенности:
1. Категориальные данные. Это данные по типу нашего примера выше (пойду на гольф или не пойду), данные с определенным категорийным ярлыком. ID3 не может использовать численные данные.
2. Информационная энтропия — индикатор, который указывает на последовательность данных с наименьшей дисперсией свойств класса значений.
1.2.1 Об использовании численных данных
Алгоритм С4.5, который является более продвинутой версией ID3, может использовать численные данные, но так как базовая идея такая же, в этой серии статей, мы, для начала, будет использовать ID3.
1.3 Среда разработки
Программа, которую я описал ниже, я проверил и запустил в следующих условиях:
・Jupyter Notebooks (с использованием Azure Notebooks)
・Python 3.6
・Библиотеки: math, pandas, functools (не использовал scikit-learn, tensorflow и т.д.)
1.4 Пример программы
1.4.1 Собственно, программа
Для начала, скопируем программу в Jupyter Notebook и запустим.
import math
import pandas as pd
from functools import reduce
# Дата сет
d = {
"Погода":["ясно","ясно","облачно","дождь","дождь","дождь","облачно","ясно","ясно","дождь","ясно","облачно","облачно","дождь"],
"Температура":["Жарко","Жарко","Жарко","Тепло","Холодно","Холодно","Холодно","Тепло","Холодно","Тепло","Тепло","Тепло","Жарко","Тепло"],
"Влажность":["Высокая","Высокая","Высокая","Высокая","Норм","Норм","Норм","Высокая","Норм","Норм","Норм","Высокая","Норм","Высокая"],
"Ветер":["Нет","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Есть"],
# Последний массив - это наша целевая переменная, показывающая результат,
# основывающийся на предыдущих данных.
"Гольф":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"],
}
df0 = pd.DataFrame(d)
# Лямбда-выражение для распределения значений, аргумент - pandas.Series,
# возвращаемое значение - массив с количеством каждого из значений
# Из вводных данных s с помощью value_counts() находим частоту каждого из значений,
# и пока в нашем словаре есть элементы, будет работать цикл, запускаемый items().
# Чтобы выходные данные не менялись с каждым запуском цикла, мы используем sorted,
# который меняет порядок от большего к меньшему
# В итоге, генерируется массив, содержащий строку из следующих компонентов: ключ (k) и значение (v).
cstr = lambda s:[k+":"+str(v) for k,v in sorted(s.value_counts().items())]
# Структура данных Decision Tree
tree = {
# name: Название этого нода (узла)
"name":"decision tree "+df0.columns[-1]+" "+str(cstr(df0.iloc[:,-1])),
# df: Данные, связанные с этим нодом (узлом)
"df":df0,
# edges: Список ребер (ветвей), выходящих из этого узла,
# или пустой массив, если ниже нет листового узла.
"edges":[],
}
# Генерацию дерева, у узлов которого могут быть ветви, сохраняем в open
open = [tree]
# Лямба-выражение для вычесления энтропии.
# Аргумент - pandas.Series、возвращаемое значение - число энтропии
entropy = lambda s:-reduce(lambda x,y:x+y,map(lambda x:(x/len(s))*math.log2(x/len(s)),s.value_counts()))
# Зацикливаем, пока open не станет пустым
while(len(open)!=0):
# Вытаскиваем из массива open первый элемент,
# и вытаскиваем данные, хранящиеся в этом узле
n = open.pop(0)
df_n = n["df"]
# В случае, если энтропия этого узла равна 0, мы больше не можем вырастить из него новые ветви
# поэтому прекращаем ветвление от этого узла
if 0==entropy(df_n.iloc[:,-1]):
continue
# Создаем переменную, в которую будем сохранять список значений атрибута с возможностью разветвления
attrs = {}
# Исследуем все атрибуты, кроме последнего столбца класса атрибутов
for attr in df_n.columns[:-1]:
# Создаем переменную, которая хранит значение энтропии при ветвлении с этим атрибутом,
# данные после разветвления и значение атрибута, который разветвляется.
attrs[attr] = {"entropy":0,"dfs":[],"values":[]}
# Исследуем все возможные значения этого атрибута.
# Кроме того, sorted предназначен для предотвращения изменения порядка массива,
# из которого были удалены повторяющиеся значения атрибутов, при каждом его выполнении.
for value in sorted(set(df_n[attr])):
# Фильтруем данные по значению атрибута
df_m = df_n.query(attr+"=='"+value+"'")
# Высчитываем энтропию, данные и значения сохрнаяем
attrs[attr]["entropy"] += entropy(df_m.iloc[:,-1])*df_m.shape[0]/df_n.shape[0]
attrs[attr]["dfs"] += [df_m]
attrs[attr]["values"] += [value]
pass
pass
# Если не осталось ни одного атрибута, значение которого можно разделить,
# прерываем исследование этого узла.
if len(attrs)==0:
continue
# Получаем атрибут с наименьшим значением энтропии
attr = min(attrs,key=lambda x:attrs[x]["entropy"])
# Добавляем каждое значение разветвленного атрибута
# и данные, полученные после разветвления, в наше дерево и в open.
for d,v in zip(attrs[attr]["dfs"],attrs[attr]["values"]):
m = {"name":attr+"="+v,"edges":[],"df":d.drop(columns=attr)}
n["edges"].append(m)
open.append(m)
pass
# Выводим дата сет
print(df0,"\n-------------")
# Метод преобразования дерева в символы, аргуметы - tree:структура данных древа,
# indent:присоединяймый к дочернему узлу indent,
# Возвращаемое значение - символьное представление древа.
# Этот метод вызывается рекурсивно для преобразования всех данных в дереве в символы.
def tstr(tree,indent=""):
# Создаем символьное представление этого узла.
# Если этот узел является листовым узлом (количество элементов в массиве ребер равно 0),
# частотное распределение последнего столбца данных df, связанных с деревом, преобразуется в символы.
s = indent+tree["name"]+str(cstr(tree["df"].iloc[:,-1]) if len(tree["edges"])==0 else "")+"\n"
# Зацикливаем все ветви этого узла.
for e in tree["edges"]:
# Добавляем символьное представление дочернего узла к символьному представлению родительского узла.
# Добавляем еще больше символов к indent этого узла.
s += tstr(e,indent+" ")
pass
return s
# Выводим древо в его символьном представлении.
print(tstr(tree))
1.4.2 Результат
Если запустить вышеописанную программу, наш Decision Tree будет представлен в виде символьной таблицы, как показано ниже.
decision tree Гольф ['×:5', '○:9']
Погода=Ясно
Влажность=Обычная['○:2']
Влажность=Высокая['×:3']
Погода=Облачно['○:4']
Погода=Дождь
Ветер=Есть['×:2']
Ветер=Нет['○:3']
1.4.3 Меняем атрибуты (массивы данных), которые хотим исследовать
Последний массив в дата сете d — это атрибут класса (массив данных, который хотим классифицировать).
d = {
"Погода":["ясно","ясно","облачно","дождь","дождь","дождь","облачно","ясно","ясно","дождь","ясно","облачно","облачно","дождь"],
"Температура":["Жарко","Жарко","Жарко","Тепло","Холодно","Холодно","Холодно","Тепло","Холодно","Тепло","Тепло","Тепло","Жарко","Тепло"],
"Влажность":["Высокая","Высокая","Высокая","Высокая","Норм","Норм","Норм","Высокая","Норм","Норм","Норм","Высокая","Норм","Высокая"],
"Гольф":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"],}
# Последний массив - это наша целевая переменная, показывающая результат, основывающийся на предыдущих данных.
"Ветер":["Нет","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Есть"],
}
Например, если поменять местами массивы “Гольф” и “Ветер”, как указано на примере выше, получится следующий результат:
decision tree Ветер ['Есть:6', 'Нет:8']
Гольф=×
Погода=ясно
Температура=Жарко
Влажность=Высокая['Есть:1', 'Нет:1']
Температура=Тепло['Нет:1']
Погода=Дождь['Есть:2']
Гольф=○
Погода=ясно
Температура=Тепло['Есть:1']
Температура=Холодно['Нет:1']
Погода=облачно
Температура=Жарко['Нет:2']
Температура=Тепло['Есть:1']
Температура=Холодно['Есть:1']
Погода=Дождь['Нет:3']
По сути, мы создаем правило, при котором сообщаем программе, что разветвляться нужно сначала по наличию и отсутствию ветра и по тому, идем играть в гольф или нет.
Спасибо за прочтение!
Мы будем очень рады, если вы расскажете нам, понравилась ли вам данная статья, понятен ли перевод, была ли она вам полезна?
===========
Источник:
habr.com
===========
===========
Автор оригинала: 豊久 中田
===========Похожие новости:
- [Программирование, Системы сборки] Make на мыло, redo сила
- [Python, Тестирование IT-систем, Тестирование веб-сервисов] Тесты в Python: все основные подходы, плюсы и минусы. Доклад Яндекса
- [Data Engineering, Data Mining, Искусственный интеллект, Машинное обучение] Отбор признаков в машинном обучении (перевод)
- [Анализ и проектирование систем, Программирование] Мама, кажется я архитектор
- [Алгоритмы, Высокая производительность, Математика, Программирование] Динамическая балансировка нагрузки в pull-схеме
- [Python, Функциональное программирование] Функциональное программирование в питоне. Генераторы, как питонячий декларативный стиль
- [Python, Алгоритмы, Лайфхаки для гиков, Научно-популярное, Программирование] Определяем пульс по вебкамере в 50 строчек кода
- [Машинное обучение] Частотный анализ русского текста и облако слов на Python
- [.NET, ASP, C#, Программирование, Тестирование IT-систем] Я десять лет страдал от ужасных архитектур в C# приложениях — и вот нашел, как их исправить
- [JavaScript, Программирование, Разработка веб-сайтов] JavaScript: область видимости простыми словами (перевод)
Теги для поиска: #_python, #_programmirovanie (Программирование), #_python, #_decision_tree, #_data_science, #_python, #_programmirovanie (
Программирование
)
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 11-Фев 17:02
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 8 лет |
|
|
Привет, Хабр! Представляю вашему вниманию перевод статьи "Pythonで0からディシジョンツリーを作って理解する (1. 概要編)". 1.1 Что такое Decision Tree? 1.1.1 Пример Decision Tree Например, у нас есть следующий набор данных (дата сет): погода, температура, влажность, ветер, игра в гольф. В зависимости от погоды и остального, мы ходили (〇) или не ходили (×) играть в гольф. Предположим, что у нас есть 14 сложившихся вариантов.  Из этих данных мы можем составить структуру данных, показывающую, в каких случаях мы шли на гольф. Такая структура из-за своей ветвистой формы называется Decision Tree.  Например, если посмотреть на Decision Tree, изображенный на картинке выше, мы поймем, что сначала проверяли погоду. Если было ясно, мы проверяли влажность: если она высокая, то не шли играть в гольф, если низкая — шли. А если погода была облачная, то шли играть в гольф вне зависимости от других условий. 1.1.2 Об этой статье Существуют алгоритмы, которые создают такие Decision Tree автоматически, на основе имеющихся данных. В этой статье мы будем использовать алгоритм ID3 на Python. Эта статья — первая из серии. Следующие статьи: (Прим. переводчика: “если вас заинтересует продолжение, пожалуйста, сообщите нам в в комментариях”.) ・Основы программирования на Python ・Необходимые основы библиотеки для анализа данных Pandas ・Основы структуры данных (в случае с Decision Tree) ・Основы информационной энтропии ・Учим алгоритм для генерации Decision Tree 1.1.3 Немного о Decision Tree Генерация Decision Tree связана с машинным обучением с учителем и классификацией. Классификация в машинном обучении — способ, позволяющий создать модель, ведущую к правильному ответу, на основе обучении на дата сете с правильными ответами и ведущими к ним данными. Глубокое обучение (Deep Learning), которое в последние годы очень популярно, особенно в сфере распознавания изображений, тоже является частью машинного обучения на основе классификационного метода. Разница Deep Learning и Decision Tree в том, приводится ли конечный результат к форме, при которой человек понимает принципы генерации конечной структуры данных. Особенность Deep Learning — мы получаем конечный результат, но не понимаем принцип его генерации. В отличие от Deep Learning, принцип построения Decision Tree прост для понимания человеком, что также является его важной особенностью. Эта особенность Decision Tree хороша не только для машинного обучения, но и дата майнинга, где также важно понимание данных пользователем. 1.2 Об алгоритме ID3 ID3 — алгоритм генерации Decision Tree, разработанный в 1986 году Россом Куинланом. У него есть две важные особенности: 1. Категориальные данные. Это данные по типу нашего примера выше (пойду на гольф или не пойду), данные с определенным категорийным ярлыком. ID3 не может использовать численные данные. 2. Информационная энтропия — индикатор, который указывает на последовательность данных с наименьшей дисперсией свойств класса значений. 1.2.1 Об использовании численных данных Алгоритм С4.5, который является более продвинутой версией ID3, может использовать численные данные, но так как базовая идея такая же, в этой серии статей, мы, для начала, будет использовать ID3. 1.3 Среда разработки Программа, которую я описал ниже, я проверил и запустил в следующих условиях: ・Jupyter Notebooks (с использованием Azure Notebooks) ・Python 3.6 ・Библиотеки: math, pandas, functools (не использовал scikit-learn, tensorflow и т.д.) 1.4 Пример программы 1.4.1 Собственно, программа Для начала, скопируем программу в Jupyter Notebook и запустим. import math
import pandas as pd from functools import reduce # Дата сет d = { "Погода":["ясно","ясно","облачно","дождь","дождь","дождь","облачно","ясно","ясно","дождь","ясно","облачно","облачно","дождь"], "Температура":["Жарко","Жарко","Жарко","Тепло","Холодно","Холодно","Холодно","Тепло","Холодно","Тепло","Тепло","Тепло","Жарко","Тепло"], "Влажность":["Высокая","Высокая","Высокая","Высокая","Норм","Норм","Норм","Высокая","Норм","Норм","Норм","Высокая","Норм","Высокая"], "Ветер":["Нет","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Есть"], # Последний массив - это наша целевая переменная, показывающая результат, # основывающийся на предыдущих данных. "Гольф":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"], } df0 = pd.DataFrame(d) # Лямбда-выражение для распределения значений, аргумент - pandas.Series, # возвращаемое значение - массив с количеством каждого из значений # Из вводных данных s с помощью value_counts() находим частоту каждого из значений, # и пока в нашем словаре есть элементы, будет работать цикл, запускаемый items(). # Чтобы выходные данные не менялись с каждым запуском цикла, мы используем sorted, # который меняет порядок от большего к меньшему # В итоге, генерируется массив, содержащий строку из следующих компонентов: ключ (k) и значение (v). cstr = lambda s:[k+":"+str(v) for k,v in sorted(s.value_counts().items())] # Структура данных Decision Tree tree = { # name: Название этого нода (узла) "name":"decision tree "+df0.columns[-1]+" "+str(cstr(df0.iloc[:,-1])), # df: Данные, связанные с этим нодом (узлом) "df":df0, # edges: Список ребер (ветвей), выходящих из этого узла, # или пустой массив, если ниже нет листового узла. "edges":[], } # Генерацию дерева, у узлов которого могут быть ветви, сохраняем в open open = [tree] # Лямба-выражение для вычесления энтропии. # Аргумент - pandas.Series、возвращаемое значение - число энтропии entropy = lambda s:-reduce(lambda x,y:x+y,map(lambda x:(x/len(s))*math.log2(x/len(s)),s.value_counts())) # Зацикливаем, пока open не станет пустым while(len(open)!=0): # Вытаскиваем из массива open первый элемент, # и вытаскиваем данные, хранящиеся в этом узле n = open.pop(0) df_n = n["df"] # В случае, если энтропия этого узла равна 0, мы больше не можем вырастить из него новые ветви # поэтому прекращаем ветвление от этого узла if 0==entropy(df_n.iloc[:,-1]): continue # Создаем переменную, в которую будем сохранять список значений атрибута с возможностью разветвления attrs = {} # Исследуем все атрибуты, кроме последнего столбца класса атрибутов for attr in df_n.columns[:-1]: # Создаем переменную, которая хранит значение энтропии при ветвлении с этим атрибутом, # данные после разветвления и значение атрибута, который разветвляется. attrs[attr] = {"entropy":0,"dfs":[],"values":[]} # Исследуем все возможные значения этого атрибута. # Кроме того, sorted предназначен для предотвращения изменения порядка массива, # из которого были удалены повторяющиеся значения атрибутов, при каждом его выполнении. for value in sorted(set(df_n[attr])): # Фильтруем данные по значению атрибута df_m = df_n.query(attr+"=='"+value+"'") # Высчитываем энтропию, данные и значения сохрнаяем attrs[attr]["entropy"] += entropy(df_m.iloc[:,-1])*df_m.shape[0]/df_n.shape[0] attrs[attr]["dfs"] += [df_m] attrs[attr]["values"] += [value] pass pass # Если не осталось ни одного атрибута, значение которого можно разделить, # прерываем исследование этого узла. if len(attrs)==0: continue # Получаем атрибут с наименьшим значением энтропии attr = min(attrs,key=lambda x:attrs[x]["entropy"]) # Добавляем каждое значение разветвленного атрибута # и данные, полученные после разветвления, в наше дерево и в open. for d,v in zip(attrs[attr]["dfs"],attrs[attr]["values"]): m = {"name":attr+"="+v,"edges":[],"df":d.drop(columns=attr)} n["edges"].append(m) open.append(m) pass # Выводим дата сет print(df0,"\n-------------") # Метод преобразования дерева в символы, аргуметы - tree:структура данных древа, # indent:присоединяймый к дочернему узлу indent, # Возвращаемое значение - символьное представление древа. # Этот метод вызывается рекурсивно для преобразования всех данных в дереве в символы. def tstr(tree,indent=""): # Создаем символьное представление этого узла. # Если этот узел является листовым узлом (количество элементов в массиве ребер равно 0), # частотное распределение последнего столбца данных df, связанных с деревом, преобразуется в символы. s = indent+tree["name"]+str(cstr(tree["df"].iloc[:,-1]) if len(tree["edges"])==0 else "")+"\n" # Зацикливаем все ветви этого узла. for e in tree["edges"]: # Добавляем символьное представление дочернего узла к символьному представлению родительского узла. # Добавляем еще больше символов к indent этого узла. s += tstr(e,indent+" ") pass return s # Выводим древо в его символьном представлении. print(tstr(tree)) 1.4.2 Результат Если запустить вышеописанную программу, наш Decision Tree будет представлен в виде символьной таблицы, как показано ниже. decision tree Гольф ['×:5', '○:9']
Погода=Ясно Влажность=Обычная['○:2'] Влажность=Высокая['×:3'] Погода=Облачно['○:4'] Погода=Дождь Ветер=Есть['×:2'] Ветер=Нет['○:3'] 1.4.3 Меняем атрибуты (массивы данных), которые хотим исследовать Последний массив в дата сете d — это атрибут класса (массив данных, который хотим классифицировать). d = {
"Погода":["ясно","ясно","облачно","дождь","дождь","дождь","облачно","ясно","ясно","дождь","ясно","облачно","облачно","дождь"], "Температура":["Жарко","Жарко","Жарко","Тепло","Холодно","Холодно","Холодно","Тепло","Холодно","Тепло","Тепло","Тепло","Жарко","Тепло"], "Влажность":["Высокая","Высокая","Высокая","Высокая","Норм","Норм","Норм","Высокая","Норм","Норм","Норм","Высокая","Норм","Высокая"], "Гольф":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"],} # Последний массив - это наша целевая переменная, показывающая результат, основывающийся на предыдущих данных. "Ветер":["Нет","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Нет","Нет","Есть","Есть","Нет","Есть"], } Например, если поменять местами массивы “Гольф” и “Ветер”, как указано на примере выше, получится следующий результат: decision tree Ветер ['Есть:6', 'Нет:8']
Гольф=× Погода=ясно Температура=Жарко Влажность=Высокая['Есть:1', 'Нет:1'] Температура=Тепло['Нет:1'] Погода=Дождь['Есть:2'] Гольф=○ Погода=ясно Температура=Тепло['Есть:1'] Температура=Холодно['Нет:1'] Погода=облачно Температура=Жарко['Нет:2'] Температура=Тепло['Есть:1'] Температура=Холодно['Есть:1'] Погода=Дождь['Нет:3'] По сути, мы создаем правило, при котором сообщаем программе, что разветвляться нужно сначала по наличию и отсутствию ветра и по тому, идем играть в гольф или нет. Спасибо за прочтение! Мы будем очень рады, если вы расскажете нам, понравилась ли вам данная статья, понятен ли перевод, была ли она вам полезна? =========== Источник: habr.com =========== =========== Автор оригинала: 豊久 中田 ===========Похожие новости:
Программирование ) |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 11-Фев 17:02
Часовой пояс: UTC + 5
