[Математика, Машинное обучение, Будущее здесь] Ученые создали машину для изобретения математики
Автор
Сообщение
news_bot ®
Стаж: 7 лет 11 месяцев
Сообщений: 27286
Хорошая гипотеза притягивает ум математика. Она говорит о чем-то сложном и глубоком точно и лаконично, требуя доказательства или опровержения. Перед хорошей формулой тяжело устоять.
Но выдвинуть красивую гипотезу сложно. Все самые элегантные и естественные, вроде гипотезы Эйлера, теоремы Ферма, формулы Римана — были предложены ещё сотни лет назад. Для развития математики ей нужны новые проблемы. И новые формулы, доказательства к которым можно было бы находить.
Для этого группа исследователей из института Технион в Израиле вместе с Google создала автоматизированную систему генерации математических гипотез. Её назвали «Машиной Рамануджана» — в честь знаменитого математика начала XX века, разработавшего тысячи новаторских формул почти без формального обучения. Программа уже выдвинула несколько оригинальных и важных уравнений для некоторых математических констант, а вокруг машины уже развивается активное математическое сообщество. Научный труд ученых был опубликован на прошлой неделе в журнале Nature.

Сриниваса Рамануджан — в центре
Машина Рамануджана не берет на себя доказательство гипотез. Она предназначена быть своего рода «кормушкой» для существующих математиков. Как объясняют исследователи в своей статье, всю отрасль математики можно, грубо говоря, разбить на два процесса: предположения и доказательства. Чем больше гипотез — тем больше материи для развития математического ума, поводов для проведения дальнейших математических исследований. Но находить их сейчас человеку почти невозможно, нужна огромная удача. Без помощи алгоритмов на составление одной красивой, полезной и правдоподобной формулы может уйти несколько десятков лет.
Ученые в своей статье говорят, что особенно полезными при поиске гипотез оказались два алгоритма: метод встречи посередине и алгоритм оптимизации градиентного спуска. Они оба работают путем сопоставления ожидаемых и полученных числовых значений. Машина строит гипотезы о формулах, не зная, есть ли у них решения, и не опираясь ни на какие предыдущие знания. Она просто «чувствует», что формула подходящая, и видит, что она хорошо предсказывает требуемый результат.

Записки Рамануджана, начало XX века
Исследователи из Техниона говорят, что их алгоритмы «могут заменить интуицию великих математиков, и открыть новые проблемы для будущих поколений». Сейчас машина выдвигает предположения о формулах, идеально описывающих значения универсальных иррациональных математических констант (например, Пи, e, φ, постоянной Апери, G, γ, log(2) и так далее). Такие константы у неё записываются в виде непрерывных дробей — то есть, дробей, знаменатель которых состоит из суммы двух членов, второй из которых сам является дробью, знаменатель которой тоже содержит два члена (один из которых является дробью, которая… и так до бесконечности).
Как это работает
Непрерывные дроби давно привлекают математиков сочетанием внешней простоты и внутренней глубины. Помимо того, что они «по своей природе очаровательны» эстетикой, они также полезны для определения фундаментальных свойств констант, как выяснили в марте 2020 года Роберт Доуттери-Блисс и Дорон Зейлбергер из Ратгерского университета в США.
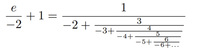
Одна из найденных формул
Машина Рамануджана находит формулы непрерывных дробей, которые с очень большой точностью кажутся равными универсальным константам. Эта высокая достоверность (вплоть до триллионных значений) — крайне важна, иначе предположения были бы легко отброшены и не имели бы большой ценности.

Каждая гипотеза принимает форму уравнения. Слева — формула, включающая универсальную константу. Справа — непрерывная дробь. Один из алгоритмов в машине проверяет их совпадение, и если чувствует, что за что-то зацепился, пытается найти более точную формулу. Второй — как обычно, пытается его опровергнуть, найдя несоответствие. Если кажется, что значения с двух сторон от знака равенства всегда совпадают, формула рассчитывается с более высокой точностью. Если ошибки не найдено, итоговая гипотеза выдается на обсуждение и решение людям.
Потом математики могут использовать эти предположения для реинжиниринга скрытых теорем или поиска более элегантных результатов, как уже показали исследования из Ратгерского университета.
Результаты
Самое заметное открытие исследователей — новая гипотеза удивительной важности. Несколько выражений (pdf), созданных Машиной, способны вычислять значение числа Каталана более эффективно, чем все предыдущие формулы, открытые человеком. Точное значение этой постоянной необходимо для решения многих математических задач.
Новые выражения в виде непрерывной дроби позволяют максимально быстро вычислить число Каталана (G). Для проверки предыдущих формул на компьютере требовалось в разы больше времени.
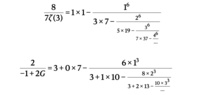
Основная работа ведется на сайте http://www.ramanujanmachine.com/. Новые найденные гипотезы добавляются в специальный раздел. На данный момент машина нашла около сорока правдоподобных гипотез для вычисления числа Пи и 25 новых формул, описывающих e, число Эйлера. А также под сотню других формул для быстрого вычисления различных иррациональных математических констант.
Как можно помочь
Исследователи пригласили математическое сообщество помочь развитию Машины Рамануджана. Сделать это можно одним из трех способов:
- Запустить машину Рамануджана у себя на компьютере. Для этого у них есть GitHub с кодом Python. Формула, найденная вашей машиной, будет названа вашим именем. Например, Пол Михальски нашел новую, ранее неизвестную формулу вычисления Пи, а Чжу Хэ — уравнение, включающее log(2). Ученые также работают над распределенным приложением на основе BOINC, которое позволит автоматически запускать машину каждый раз, когда компьютер простаивает.
- Попытаться доказать предположения машины. Алгоритмы обнаруживают математические формулы, но не доказывают их. Можно попытаться доказать их предположения и внести свой вклад в математику, отправив ссылку с PDF/DOC/TXT-файл с доказательством к ним на сайт.
- Предложить или разработать свои алгоритмы. Если у вас есть идеи по улучшению алгоритмов для поиска математических формул, можно предложить их на GitHub проекта. Разработка длится уже несколько лет, она началась задолго до официальной публикации в Nature, и команда считает, что машине ещё есть, куда расти.
Раньше компьютеры эффективнее нас решали готовые задачи. Теперь они оказались лучше людей и в составлении гипотез.

оригинал
===========
Источник:
habr.com
===========
Похожие новости:
- [Nginx, Управление проектами, Лайфхаки для гиков, Мозг] Уточняем детали проекта методами практической психологии
- [JavaScript, Node.JS, Профессиональная литература] Книга «Веб-разработка с применением Node и Express. Полноценное использование стека JavaScript. 2-е издание »
- [Python, Программирование] Разбираемся с not в Python (перевод)
- [Программирование, .NET, ASP, C#] Что из себя представляет класс Startup и Program.cs в ASP.NET Core (перевод)
- [CAD/CAM] Численное моделирование для разработки новых продуктов и технологий
- [Программирование, Функциональное программирование] Сильные стороны функционального программирования
- [Разработка веб-сайтов, PHP, Управление сообществом] Каким будет 2021-й год для PHP?
- [Венчурные инвестиции, Развитие стартапа, Финансы в IT, IT-компании] Новости IT и инвестиций: Маск покупает Bitcoin, взлет Clubhouse
- [Поисковые технологии, Управление медиа, IT-компании] Microsoft предложила обязать Google и Facebook платить за новости в США
- [Нанотехнологии] Мировой рекорд в плазмонике: созданы волноводы на основе золота с рекордной длиной распространения сигнала 250 мкм
Теги для поиска: #_matematika (Математика), #_mashinnoe_obuchenie (Машинное обучение), #_buduschee_zdes (Будущее здесь), #_matematika (математика), #_ramanudzhan (рамануджан), #_gipotezy (гипотезы), #_ii (ии), #_itsoft, #_blog_kompanii_vebstudija_i_datatsentr_itsoft (
Блог компании Веб-студия и дата-центр ITSOFT
), #_matematika (
Математика
), #_mashinnoe_obuchenie (
Машинное обучение
), #_buduschee_zdes (
Будущее здесь
)
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 15-Янв 13:16
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 11 месяцев |
|
 Хорошая гипотеза притягивает ум математика. Она говорит о чем-то сложном и глубоком точно и лаконично, требуя доказательства или опровержения. Перед хорошей формулой тяжело устоять. Но выдвинуть красивую гипотезу сложно. Все самые элегантные и естественные, вроде гипотезы Эйлера, теоремы Ферма, формулы Римана — были предложены ещё сотни лет назад. Для развития математики ей нужны новые проблемы. И новые формулы, доказательства к которым можно было бы находить. Для этого группа исследователей из института Технион в Израиле вместе с Google создала автоматизированную систему генерации математических гипотез. Её назвали «Машиной Рамануджана» — в честь знаменитого математика начала XX века, разработавшего тысячи новаторских формул почти без формального обучения. Программа уже выдвинула несколько оригинальных и важных уравнений для некоторых математических констант, а вокруг машины уже развивается активное математическое сообщество. Научный труд ученых был опубликован на прошлой неделе в журнале Nature.  Сриниваса Рамануджан — в центре Машина Рамануджана не берет на себя доказательство гипотез. Она предназначена быть своего рода «кормушкой» для существующих математиков. Как объясняют исследователи в своей статье, всю отрасль математики можно, грубо говоря, разбить на два процесса: предположения и доказательства. Чем больше гипотез — тем больше материи для развития математического ума, поводов для проведения дальнейших математических исследований. Но находить их сейчас человеку почти невозможно, нужна огромная удача. Без помощи алгоритмов на составление одной красивой, полезной и правдоподобной формулы может уйти несколько десятков лет. Ученые в своей статье говорят, что особенно полезными при поиске гипотез оказались два алгоритма: метод встречи посередине и алгоритм оптимизации градиентного спуска. Они оба работают путем сопоставления ожидаемых и полученных числовых значений. Машина строит гипотезы о формулах, не зная, есть ли у них решения, и не опираясь ни на какие предыдущие знания. Она просто «чувствует», что формула подходящая, и видит, что она хорошо предсказывает требуемый результат.  Записки Рамануджана, начало XX века Исследователи из Техниона говорят, что их алгоритмы «могут заменить интуицию великих математиков, и открыть новые проблемы для будущих поколений». Сейчас машина выдвигает предположения о формулах, идеально описывающих значения универсальных иррациональных математических констант (например, Пи, e, φ, постоянной Апери, G, γ, log(2) и так далее). Такие константы у неё записываются в виде непрерывных дробей — то есть, дробей, знаменатель которых состоит из суммы двух членов, второй из которых сам является дробью, знаменатель которой тоже содержит два члена (один из которых является дробью, которая… и так до бесконечности). Как это работает Непрерывные дроби давно привлекают математиков сочетанием внешней простоты и внутренней глубины. Помимо того, что они «по своей природе очаровательны» эстетикой, они также полезны для определения фундаментальных свойств констант, как выяснили в марте 2020 года Роберт Доуттери-Блисс и Дорон Зейлбергер из Ратгерского университета в США. 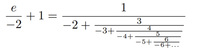 Одна из найденных формул Машина Рамануджана находит формулы непрерывных дробей, которые с очень большой точностью кажутся равными универсальным константам. Эта высокая достоверность (вплоть до триллионных значений) — крайне важна, иначе предположения были бы легко отброшены и не имели бы большой ценности.  Каждая гипотеза принимает форму уравнения. Слева — формула, включающая универсальную константу. Справа — непрерывная дробь. Один из алгоритмов в машине проверяет их совпадение, и если чувствует, что за что-то зацепился, пытается найти более точную формулу. Второй — как обычно, пытается его опровергнуть, найдя несоответствие. Если кажется, что значения с двух сторон от знака равенства всегда совпадают, формула рассчитывается с более высокой точностью. Если ошибки не найдено, итоговая гипотеза выдается на обсуждение и решение людям. Потом математики могут использовать эти предположения для реинжиниринга скрытых теорем или поиска более элегантных результатов, как уже показали исследования из Ратгерского университета. Результаты Самое заметное открытие исследователей — новая гипотеза удивительной важности. Несколько выражений (pdf), созданных Машиной, способны вычислять значение числа Каталана более эффективно, чем все предыдущие формулы, открытые человеком. Точное значение этой постоянной необходимо для решения многих математических задач. Новые выражения в виде непрерывной дроби позволяют максимально быстро вычислить число Каталана (G). Для проверки предыдущих формул на компьютере требовалось в разы больше времени.  Основная работа ведется на сайте http://www.ramanujanmachine.com/. Новые найденные гипотезы добавляются в специальный раздел. На данный момент машина нашла около сорока правдоподобных гипотез для вычисления числа Пи и 25 новых формул, описывающих e, число Эйлера. А также под сотню других формул для быстрого вычисления различных иррациональных математических констант. Как можно помочь Исследователи пригласили математическое сообщество помочь развитию Машины Рамануджана. Сделать это можно одним из трех способов:
Раньше компьютеры эффективнее нас решали готовые задачи. Теперь они оказались лучше людей и в составлении гипотез.  оригинал =========== Источник: habr.com =========== Похожие новости:
Блог компании Веб-студия и дата-центр ITSOFT ), #_matematika ( Математика ), #_mashinnoe_obuchenie ( Машинное обучение ), #_buduschee_zdes ( Будущее здесь ) |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 15-Янв 13:16
Часовой пояс: UTC + 5
