[Data Engineering] Что такое фильтр Блума? (перевод)
Автор
Сообщение
news_bot ®
Стаж: 7 лет 8 месяцев
Сообщений: 27286

Всем привет! В этой статье я постараюсь описать, что такое фильтр Блума, рассказать о его назначении и показать сценарии, в которых его можно использовать. Я также реализую фильтр Блума на Python с нуля в целях облегчения понимания его внутреннего устройства.Назначение фильтра Блума Фильтр Блума — это структура данных, цель которой — быстро проверить, что элемент НЕ входит в множество (для тех, кто знаком с нотацией O большое, сложность вставки и проверки принадлежности элемента к множеству с помощью фильтра Блума — O(1)). Он может быть очень полезен для предотвращения излишнего выполнения задач, требующих интенсивных вычислений, просто проверяя, что элемент совершенно точно не входит в множество. Важно понимать, что фильтр Блума — это вероятностная структура данных: он может сказать вам со 100% вероятностью, что элемент отсутствует в наборе данных, но сказать со 100% вероятностью, что элемент находится в наборе, он не может (возможны ложно положительные результаты). Давайте же поговорим о сценариях, в которых можно использовать фильтр Блума с подробным объяснением его внутреннего устройства и реализацией на Python, и позже вы поймете, откуда фильтр Блума имеет такие показатели!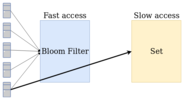
Фильтр Блума обычно используется перед поиском в множестве с достаточно медленным доступом к элементам. За счет его использования может быть уменьшено как количество поисковых операций над множеством, так и время поиска в целом.Сценарии использованияДавайте поразмыслим о сценариях, в которых для ускорения вычисления некоторых задач такая структура данных могла бы оказаться очень полезной. Например, мы можем начать с маршрутизатора опорной сети (не такого, который вы можете найти у себя дома). От таких маршрутизаторов может требоваться скорость в uplink более 100 Гбит/с. Администратору может понадобиться создать черный список IP-адресов, чтобы заблокировать им доступ в сеть. Это означает, что каждый раз, когда маршрутизатор получает пакет на скорости более 100 Гбит/с, он должен обращаться к своей памяти и выполнять в лучшем случае логарифмический поиск (O(log(n))), чтобы проверить, заблокирован ли IP-адрес, учитывая, что большинство IP-адресов не заблокированы и что поиск не даст результатов для большинства пакетов. В этом случае фильтр Блума может быть реализован как раз перед доступом к памяти, чтобы гарантировать, что большинству пакетов не нужно дожидаться поиска IP-адреса для отправки в сеть.Еще один сценарий — это базы данных. Когда к базе данных происходят миллионы обращений в секунду, и большинство обращений представляют из себя поиск по ключу, которого в базе данных нет, максимально уменьшить нагрузку таких обращений на базу данных может быть важно по двум причинам: если сократить количество поисков, ядро базы данных будет быстрее отвечать на другие обращения; если клиент может не дожидаться поиска по базе данных и получить результат (например, не из памяти) без необходимости доступа к базе данных, достигнутое ускорение может быть весьма существенным.Наконец, чтобы ускорить процесс поиска файла в папке с большим количеством файлов, можно использовать фильтр Блума, чтобы сначала проверить, отсутствует ли файл в этой папке.Более типичные сценарии использования фильтра Блума можно найти здесь.Что из себя представляет фильтр Блума?Чтобы проиллюстрировать устройство фильтра Блума, мы будем использовать первый сценарий. Представьте, что вы внесли в черный список 100 IP-адресов. Самый простой способ пометить, есть ли IP-адрес в черном списке или нет, — создать список из 100 бит, где каждый бит — это один IP. Если IP-адрес занесен в черный список, мы отмечаем его позицию как «1», в противном случае — «0».
В этом фильтре Блума 4-й IP-адрес занесен в черный список, а все остальные нет.Сколько всего IP-адресов?Эта реализация работает, если используются только 100 IP. В реальности же каждый IPv4-адрес имеет 32 бита, что означает, что существует 4 294 967 296 (2^32) возможных адресов (некоторые из них зарезервированы для приватных, бродкастных, мультикастных и других специальных сетей, но оставшихся адресов все еще огромное количество)! И количество IP-адресов в черном списке, вероятно, не превысит нескольких сотен в самом крайнем случае. Мы не можем позволить себе составлять такой большой список, чтобы использовать его для такого относительно небольшого количества записей. Нам нужно найти способ сопоставления IP-адреса и записей в списке. И вот тут-то и приходят на помощь хеш-функции.Хеш-функцияХеш-функция — это функция, которая преобразует вход произвольной длины в значение фиксированного размера. Таким образом, мы можем создать массив фиксированного размера и вычислить результат хеш-функции по конкретному IP-адресу, и он всегда будет генерировать число, меньшее или равное размеру массива. Хеш-функция не является случайной функцией, что означает, что для одного и того же ввода вывод всегда будет одинаковым.
Хеш-функция получает ввод, который может быть любой строкой (в данном случае IP), и вычисляет числовое представление. В этом случае числовое представление будет позицией в фильтре Блума, соответствующей входным данным.Но подождите… Что-то не так. Вернемся к нашему сценарию. Представьте, что мы занесли в черный список 100 IP-адресов. Как хеш-функция точно сопоставит наши 100 из возможных 2^32 IP-адресов на 100 различных значений без сохранения какой-либо информации о них? Правда в том, что никак. Будут коллизии. Хэш-функция гарантирует, что каждый IP-адрес будет иметь собственное сопоставление с числом, но, поскольку может быть 4 294 967 296 (2^32) возможных IP-адресов, невозможно сопоставить их все с всего лишь сотней различных значений. Все, что может гарантировать хеш-функция, — это то, что она скремблирует биты входных данных так, чтобы выходные данные согласовались с равномерным распределением. Это означает, что если вы измените ввод хеш-функции с 192.168.1.1 на 192.168.1.2, вывод, вероятно, будет совершенно другим, кажущимся случайным (но в действительности не случайным, поскольку каждому вводу всегда будет соответствовать один и тот же вывод).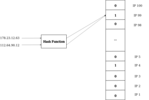
Пример коллизии. Два разных IP-адреса имеют одинаковый хеш, а это означает, что их индекс в фильтре Блума будет одинаковым.Хорошо, теперь с самого начала: мы заносим в черный список 100 IP-адресов. Каждый IP-адрес будет проходить через хеш-функцию, и результат хеш-функции вернет число, меньшее или равное размеру массива. Это число будет индексом массива, который отмечает, был ли IP-адрес в черном списке или нет. Но будут коллизии — как нам с этим справиться?Предположим, что IP-адреса 178.23.12.63 и 112.64.90.12 имеют одинаковый хеш. Первый IP попал в черный список, второй — нет. Когда мы проверяем, находится ли хеш второго IP-адреса в фильтре Блума, мы его там найдем, даже если этот IP-адрес никогда не попадал в черный список. Означает ли это, что у нас есть ошибка?Помните, что в начале я предупреждал, что цель фильтра Блума — проверить, что элемент НЕ входит в набор данных. Если позиция элемента в фильтре Блума равна 0, этот элемент определенно НЕ входит в набор. Однако, если позиция элемента в фильтре Блума равна 1, то либо этот элемент может все-таки быть в наборе, либо это просто коллизия. Все, что мы можем сделать, это уменьшить вероятность коллизии, чтобы уменьшить количество обращений к памяти, необходимых для проверки, действительно ли IP находится в черном списке.Снижение вероятности коллизийЕсть два основных способа снизить вероятность коллизий, и оба с нюансами. Одна из возможностей — увеличить размер массива. Если мы увеличим размер массива (и, следовательно, заставим хеш-функцию возвращать число меньше или того же размера, что и новый размер массива), вероятность коллизий уменьшается. В частности, вероятность ложного срабатывания (фильтр Блума возвращает 1, когда элемент отсутствует в наборе) составляет (1-e^(m / n)), где m — количество элементов, которые предполагается внести в фильтр, а n размер фильтра.Другой способ уменьшить вероятность коллизии — увеличить количество хеш-функций. Это означает, что в нашем сценарии для одного IP-адреса будет использоваться несколько различных хеш-функций, т.е. несколько различных мест в массиве будет помечаться как 1. Если мы используем k хеш-функций, вероятность ложного срабатывания теперь (1-e^(mk/n))^k, что означает, что оптимальное количество хеш-функций равно (n/m)*ln(2) (подробнее об этих уравнениях можно почитать здесь).
Пример фильтра Блума с двумя хеш-функциями. В одном из хешей этих IP-адресов мы наблюдаем коллизию, но все-равно можно проверить, что IP 112.64.90.12 не входит в набор, потому что одна из его позиций фильтра Блума не равна 1.Ну что ж, а теперь давайте реализуем фильтр Блума в Python и посмотрим на результат! Это займет у нас всего около 50 строк кода.Давайте начнем с создания класса BloomFilter (в следующем фрагменте кода). Конструктор получает размер фильтра Блума и (это опционально) количество ожидаемых элементов, которые будет хранить этот фильтр Блума. Для создания массива из битов мы будем использовать библиотеку bitarray, и мы установим их все в ноль. Наконец, мы устанавливаем количество хеш-функций в уравнение, которое возвращает оптимальное количество хеш-функций, учитывая размер фильтра Блума и количество ожидаемых элементов.
import math
from bitarray import bitarray
class BloomFilter(object):
def __init__(self, size, number_expected_elements=100000):
self.size = size
self.number_expected_elements = number_expected_elements
self.bloom_filter = bitarray(self.size)
self.bloom_filter.setall(0)
self.number_hash_functions = round((self.size / self.number_expected_elements) * math.log(2))
Теперь давайте определим хеш-функцию для фильтра Блума. Используемая реализация (взятая отсюда) реализует алгоритм DJB2. Сейчас мы будем использовать его как черный ящик, поскольку объяснение это алгоритма выходит за рамки темы этой статьи.
def _hash_djb2(self, s):
hash = 5381
for x in s:
hash = ((hash << 5) + hash) + ord(x)
return hash % self.size
Теперь у нас есть хеш-функция, но как нам создать K хеш-функций? Мы можем сделать один простой фокус. Вместо того, чтобы создавать разные хеш-функции, мы просто будем добавлять число к каждому вводу в хеш-функцию. Число будет представлять из себя номер вызываемой хэш-функции. Поскольку любая небольшая разница во вводе хеш-функции результирует в совершенно другом хеше, результат можно рассматривать как другую хеш-функцию. Круто, правда?
def _hash(self, item, K):
return self._hash_djb2(str(K) + item)
Теперь давайте создадим функцию для добавления элемента в фильтр Блума. Для этого давайте проитерируем все хеш-функции, вычисляя хеш для элемента и, наконец, помещая 1 (или True) в индекс хеша.
def add_to_filter(self, item):
for i in range(self.number_hash_functions):
self.bloom_filter[self._hash(item, i)] = 1
Осталось только создать функцию, которая проверяет, что элемент НЕ находится в фильтре Блума. Для этого давайте еще раз проитерируем по всем хеш-функциям. Если какая-либо из позиций фильтра Блума имеет 0, мы можем сказать, что элемент определенно отсутствует в наборе. В противном случае, если все позиции имеют 1, мы не можем сказать, что элемента нет в наборе.
def check_is_not_in_filter(self, item):
for i in range(self.number_hash_functions):
if self.bloom_filter[self._hash(item, i)] == 0:
return True
return False
И все! Мы реализовали наш фильтр Блума. Давай протестируем его!Мы создадим простой тест, чтобы проверить, работает ли он. Давайте создадим фильтр Блума с 1 миллионом записей, а затем установим ожидаемое количество элементов равным 100 000. Мы собираемся добавить элемент «192.168.1.1» в наш фильтр Блума в качестве заблокированного IP-адреса.
bloom_filter = BloomFilter(1000000, 100000)
base_ip = "192.168.1."
bloom_filter.add_to_filter(base_ip + str(1))
Чтобы проверить это, мы будем итерировать i от 1 до 100 000 и проверять, находится ли IP 192.168.1.i в фильтре Блума (нет таких IP-адресов, где i>254, например 192.168.289, но в данном случае мы просто проводим тест). Мы выведем элементы, о которых мы не знаем, входят ли они в набор; все остальные элементы, которые не будут напечатаны, точно не входят в набор.
for i in range(1, 100000):
if not bloom_filter.check_is_not_in_filter(base_ip + str(i)):
print(base_ip+str(i))
192.168.1.1Да! Наш фильтр Блума говорит, что из 100 000 IP-адресов единственный элемент, который может быть заблокированным, — это действительно наш заблокированный IP-адрес. Никаких ложноположительных результатов!Вот полный код нашего фильтра Блума:
import math
from bitarray import bitarray
class BloomFilter(object):
def __init__(self, size, number_expected_elements=100000):
self.size = size
self.number_expected_elements = number_expected_elements
self.bloom_filter = bitarray(self.size)
self.bloom_filter.setall(0)
self.number_hash_functions = round((self.size / self.number_expected_elements) * math.log(2))
def _hash_djb2(self, s):
hash = 5381
for x in s:
hash = ((hash << 5) + hash) + ord(x)
return hash % self.size
def _hash(self, item, K):
return self._hash_djb2(str(K) + item)
def add_to_filter(self, item):
for i in range(self.number_hash_functions):
self.bloom_filter[self._hash(item, i)] = 1
def check_is_not_in_filter(self, item):
for i in range(self.number_hash_functions):
if self.bloom_filter[self._hash(item, i)] == 0:
return True
return False
bloom_filter = BloomFilter(1000000, 100000)
base_ip = "192.168.1."
bloom_filter.add_to_filter(base_ip + str(1))
for i in range(1, 100000):
if not bloom_filter.check_is_not_in_filter(base_ip + str(i)):
print(base_ip+str(i))
Вот и все, что касается фильтров Блума. Я надеюсь, что вам было интересно узнать, что такое фильтр Блума и как его реализовать. Спасибо за внимание!
Перевод статьи подготовлен в преддверии старта курса «Data Engineer».Также приглашаем всех желающих на бесплатный демо-урок по теме «ML в Spark». На занятии участники вместе с экспертом узнают об особенностях ML в Spark, рассмотрят процесс разработки моделей и научатся переводить обученные модели в production
===========
Источник:
habr.com
===========
===========
Автор оригинала: Diogo Ferreira
===========Похожие новости:
- [Математика] Новые квантовые алгоритмы, совершившие прорыв в нелинейных уравнениях (перевод)
- [Big Data] СУБД «Яндекс ClickHouse» внедрили в российскую систему предиктивной аналитики «ПРАНА»
- [SQLite, Xcode, Swift] Видеомонтаж, машинное обучение и взломанный xml — все в одной программе
- [Python, Big Data, GitHub] Я спарсил больше 1000 топовых Github-профилей по машинному обучению и вот что я узнал (перевод)
- [Программирование, Алгоритмы, Go] Algorithms in Go: Dutch National Flag
- [Google Chrome, HTML, Браузеры] Браузерные войны 2021 (перевод)
- [Python, Машинное обучение, Искусственный интеллект, Data Engineering, TensorFlow] Рецепт обучения нейросетей (перевод)
- [MySQL, Администрирование баз данных] Советы по хранению Percona Backup в облаке (перевод)
- [Программирование, Go] Создаем бессерверное приложение с помощью Azure Functions и Go (перевод)
- [Agile, Управление продуктом] Цель продукта – это промежуточная стратегическая цель (перевод)
Теги для поиска: #_data_engineering, #_ml, #_spark, #_data_engineer, #_big_data, #_bloom_filter, #_algorithms, #_data_structures, #_blog_kompanii_otus (
Блог компании OTUS
), #_data_engineering
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 28-Окт 23:07
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 8 месяцев |
|
 Всем привет! В этой статье я постараюсь описать, что такое фильтр Блума, рассказать о его назначении и показать сценарии, в которых его можно использовать. Я также реализую фильтр Блума на Python с нуля в целях облегчения понимания его внутреннего устройства.Назначение фильтра Блума Фильтр Блума — это структура данных, цель которой — быстро проверить, что элемент НЕ входит в множество (для тех, кто знаком с нотацией O большое, сложность вставки и проверки принадлежности элемента к множеству с помощью фильтра Блума — O(1)). Он может быть очень полезен для предотвращения излишнего выполнения задач, требующих интенсивных вычислений, просто проверяя, что элемент совершенно точно не входит в множество. Важно понимать, что фильтр Блума — это вероятностная структура данных: он может сказать вам со 100% вероятностью, что элемент отсутствует в наборе данных, но сказать со 100% вероятностью, что элемент находится в наборе, он не может (возможны ложно положительные результаты). Давайте же поговорим о сценариях, в которых можно использовать фильтр Блума с подробным объяснением его внутреннего устройства и реализацией на Python, и позже вы поймете, откуда фильтр Блума имеет такие показатели!  Фильтр Блума обычно используется перед поиском в множестве с достаточно медленным доступом к элементам. За счет его использования может быть уменьшено как количество поисковых операций над множеством, так и время поиска в целом.Сценарии использованияДавайте поразмыслим о сценариях, в которых для ускорения вычисления некоторых задач такая структура данных могла бы оказаться очень полезной. Например, мы можем начать с маршрутизатора опорной сети (не такого, который вы можете найти у себя дома). От таких маршрутизаторов может требоваться скорость в uplink более 100 Гбит/с. Администратору может понадобиться создать черный список IP-адресов, чтобы заблокировать им доступ в сеть. Это означает, что каждый раз, когда маршрутизатор получает пакет на скорости более 100 Гбит/с, он должен обращаться к своей памяти и выполнять в лучшем случае логарифмический поиск (O(log(n))), чтобы проверить, заблокирован ли IP-адрес, учитывая, что большинство IP-адресов не заблокированы и что поиск не даст результатов для большинства пакетов. В этом случае фильтр Блума может быть реализован как раз перед доступом к памяти, чтобы гарантировать, что большинству пакетов не нужно дожидаться поиска IP-адреса для отправки в сеть.Еще один сценарий — это базы данных. Когда к базе данных происходят миллионы обращений в секунду, и большинство обращений представляют из себя поиск по ключу, которого в базе данных нет, максимально уменьшить нагрузку таких обращений на базу данных может быть важно по двум причинам: если сократить количество поисков, ядро базы данных будет быстрее отвечать на другие обращения; если клиент может не дожидаться поиска по базе данных и получить результат (например, не из памяти) без необходимости доступа к базе данных, достигнутое ускорение может быть весьма существенным.Наконец, чтобы ускорить процесс поиска файла в папке с большим количеством файлов, можно использовать фильтр Блума, чтобы сначала проверить, отсутствует ли файл в этой папке.Более типичные сценарии использования фильтра Блума можно найти здесь.Что из себя представляет фильтр Блума?Чтобы проиллюстрировать устройство фильтра Блума, мы будем использовать первый сценарий. Представьте, что вы внесли в черный список 100 IP-адресов. Самый простой способ пометить, есть ли IP-адрес в черном списке или нет, — создать список из 100 бит, где каждый бит — это один IP. Если IP-адрес занесен в черный список, мы отмечаем его позицию как «1», в противном случае — «0».  В этом фильтре Блума 4-й IP-адрес занесен в черный список, а все остальные нет.Сколько всего IP-адресов?Эта реализация работает, если используются только 100 IP. В реальности же каждый IPv4-адрес имеет 32 бита, что означает, что существует 4 294 967 296 (2^32) возможных адресов (некоторые из них зарезервированы для приватных, бродкастных, мультикастных и других специальных сетей, но оставшихся адресов все еще огромное количество)! И количество IP-адресов в черном списке, вероятно, не превысит нескольких сотен в самом крайнем случае. Мы не можем позволить себе составлять такой большой список, чтобы использовать его для такого относительно небольшого количества записей. Нам нужно найти способ сопоставления IP-адреса и записей в списке. И вот тут-то и приходят на помощь хеш-функции.Хеш-функцияХеш-функция — это функция, которая преобразует вход произвольной длины в значение фиксированного размера. Таким образом, мы можем создать массив фиксированного размера и вычислить результат хеш-функции по конкретному IP-адресу, и он всегда будет генерировать число, меньшее или равное размеру массива. Хеш-функция не является случайной функцией, что означает, что для одного и того же ввода вывод всегда будет одинаковым.  Хеш-функция получает ввод, который может быть любой строкой (в данном случае IP), и вычисляет числовое представление. В этом случае числовое представление будет позицией в фильтре Блума, соответствующей входным данным.Но подождите… Что-то не так. Вернемся к нашему сценарию. Представьте, что мы занесли в черный список 100 IP-адресов. Как хеш-функция точно сопоставит наши 100 из возможных 2^32 IP-адресов на 100 различных значений без сохранения какой-либо информации о них? Правда в том, что никак. Будут коллизии. Хэш-функция гарантирует, что каждый IP-адрес будет иметь собственное сопоставление с числом, но, поскольку может быть 4 294 967 296 (2^32) возможных IP-адресов, невозможно сопоставить их все с всего лишь сотней различных значений. Все, что может гарантировать хеш-функция, — это то, что она скремблирует биты входных данных так, чтобы выходные данные согласовались с равномерным распределением. Это означает, что если вы измените ввод хеш-функции с 192.168.1.1 на 192.168.1.2, вывод, вероятно, будет совершенно другим, кажущимся случайным (но в действительности не случайным, поскольку каждому вводу всегда будет соответствовать один и тот же вывод).  Пример коллизии. Два разных IP-адреса имеют одинаковый хеш, а это означает, что их индекс в фильтре Блума будет одинаковым.Хорошо, теперь с самого начала: мы заносим в черный список 100 IP-адресов. Каждый IP-адрес будет проходить через хеш-функцию, и результат хеш-функции вернет число, меньшее или равное размеру массива. Это число будет индексом массива, который отмечает, был ли IP-адрес в черном списке или нет. Но будут коллизии — как нам с этим справиться?Предположим, что IP-адреса 178.23.12.63 и 112.64.90.12 имеют одинаковый хеш. Первый IP попал в черный список, второй — нет. Когда мы проверяем, находится ли хеш второго IP-адреса в фильтре Блума, мы его там найдем, даже если этот IP-адрес никогда не попадал в черный список. Означает ли это, что у нас есть ошибка?Помните, что в начале я предупреждал, что цель фильтра Блума — проверить, что элемент НЕ входит в набор данных. Если позиция элемента в фильтре Блума равна 0, этот элемент определенно НЕ входит в набор. Однако, если позиция элемента в фильтре Блума равна 1, то либо этот элемент может все-таки быть в наборе, либо это просто коллизия. Все, что мы можем сделать, это уменьшить вероятность коллизии, чтобы уменьшить количество обращений к памяти, необходимых для проверки, действительно ли IP находится в черном списке.Снижение вероятности коллизийЕсть два основных способа снизить вероятность коллизий, и оба с нюансами. Одна из возможностей — увеличить размер массива. Если мы увеличим размер массива (и, следовательно, заставим хеш-функцию возвращать число меньше или того же размера, что и новый размер массива), вероятность коллизий уменьшается. В частности, вероятность ложного срабатывания (фильтр Блума возвращает 1, когда элемент отсутствует в наборе) составляет (1-e^(m / n)), где m — количество элементов, которые предполагается внести в фильтр, а n размер фильтра.Другой способ уменьшить вероятность коллизии — увеличить количество хеш-функций. Это означает, что в нашем сценарии для одного IP-адреса будет использоваться несколько различных хеш-функций, т.е. несколько различных мест в массиве будет помечаться как 1. Если мы используем k хеш-функций, вероятность ложного срабатывания теперь (1-e^(mk/n))^k, что означает, что оптимальное количество хеш-функций равно (n/m)*ln(2) (подробнее об этих уравнениях можно почитать здесь).  Пример фильтра Блума с двумя хеш-функциями. В одном из хешей этих IP-адресов мы наблюдаем коллизию, но все-равно можно проверить, что IP 112.64.90.12 не входит в набор, потому что одна из его позиций фильтра Блума не равна 1.Ну что ж, а теперь давайте реализуем фильтр Блума в Python и посмотрим на результат! Это займет у нас всего около 50 строк кода.Давайте начнем с создания класса BloomFilter (в следующем фрагменте кода). Конструктор получает размер фильтра Блума и (это опционально) количество ожидаемых элементов, которые будет хранить этот фильтр Блума. Для создания массива из битов мы будем использовать библиотеку bitarray, и мы установим их все в ноль. Наконец, мы устанавливаем количество хеш-функций в уравнение, которое возвращает оптимальное количество хеш-функций, учитывая размер фильтра Блума и количество ожидаемых элементов. import math
from bitarray import bitarray class BloomFilter(object): def __init__(self, size, number_expected_elements=100000): self.size = size self.number_expected_elements = number_expected_elements self.bloom_filter = bitarray(self.size) self.bloom_filter.setall(0) self.number_hash_functions = round((self.size / self.number_expected_elements) * math.log(2)) def _hash_djb2(self, s):
hash = 5381 for x in s: hash = ((hash << 5) + hash) + ord(x) return hash % self.size def _hash(self, item, K):
return self._hash_djb2(str(K) + item) def add_to_filter(self, item):
for i in range(self.number_hash_functions): self.bloom_filter[self._hash(item, i)] = 1 def check_is_not_in_filter(self, item):
for i in range(self.number_hash_functions): if self.bloom_filter[self._hash(item, i)] == 0: return True return False bloom_filter = BloomFilter(1000000, 100000)
base_ip = "192.168.1." bloom_filter.add_to_filter(base_ip + str(1)) for i in range(1, 100000):
if not bloom_filter.check_is_not_in_filter(base_ip + str(i)): print(base_ip+str(i)) import math
from bitarray import bitarray class BloomFilter(object): def __init__(self, size, number_expected_elements=100000): self.size = size self.number_expected_elements = number_expected_elements self.bloom_filter = bitarray(self.size) self.bloom_filter.setall(0) self.number_hash_functions = round((self.size / self.number_expected_elements) * math.log(2)) def _hash_djb2(self, s): hash = 5381 for x in s: hash = ((hash << 5) + hash) + ord(x) return hash % self.size def _hash(self, item, K): return self._hash_djb2(str(K) + item) def add_to_filter(self, item): for i in range(self.number_hash_functions): self.bloom_filter[self._hash(item, i)] = 1 def check_is_not_in_filter(self, item): for i in range(self.number_hash_functions): if self.bloom_filter[self._hash(item, i)] == 0: return True return False bloom_filter = BloomFilter(1000000, 100000) base_ip = "192.168.1." bloom_filter.add_to_filter(base_ip + str(1)) for i in range(1, 100000): if not bloom_filter.check_is_not_in_filter(base_ip + str(i)): print(base_ip+str(i)) Перевод статьи подготовлен в преддверии старта курса «Data Engineer».Также приглашаем всех желающих на бесплатный демо-урок по теме «ML в Spark». На занятии участники вместе с экспертом узнают об особенностях ML в Spark, рассмотрят процесс разработки моделей и научатся переводить обученные модели в production
=========== Источник: habr.com =========== =========== Автор оригинала: Diogo Ferreira ===========Похожие новости:
Блог компании OTUS ), #_data_engineering |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 28-Окт 23:07
Часовой пояс: UTC + 5
