[Алгоритмы, Математика, Машинное обучение, Искусственный интеллект] Алгоритм обучения нейронных сетей с помощью нового вида чисел

Ответить на тему

Автор

Сообщение

news_bot ^®

Стаж: 6 лет 9 месяцев
Сообщений: 27286

news_bot ^® написал(а)
13-Янв-2021 16:31

Цитировать

Приветствую читатель. Когда я был ребёнком и учился в школе, моим любимым предметом была математика, любимым предметом она была из-за того, что я очень люблю решать задачи, в какой-то момент своей жизни я начал составлять сам для себя заведомо нерешаемые задачи и пытался их решить, по полной напрягая свой разум в продумывании подхода для решения нерешаемой задачи, иногда оказывалось, что нерешаемая задача только казалась таковой из-за упущения некоторых неочевидных моментов. Любовь к решению задач сильно повлияла на меня, из-за чего я у себя в голове постоянно решаю какие-либо задачи, не только математические, но и из других сфер. За жизнь у меня накопилось множество идей (решений), от 3d принтера печатающего сталью до способа решения проблемы утилизации радиоактивных отходов атомных электростанций. Наверняка многие идеи на самом деле не реализуемы, по тем или иным причинам, а некоторые наверняка были придуманы до меня, а я просто о них не знал (так уже бывало). В прошлой моей статье я упомянул (сам не знаю зачем) о том, что я придумал новый вид чисел с помощью которых можно обучать нейронные сети. Я хотел открыть сервис по обучению нейронных сетей с помощью этих чисел, но с учётом пандемии и моего плохого состояния здоровья, я подумал, что вдруг я реально первый кто додумался до этих чисел и будет крайне плохо если я умру и знания о этих числах уйдут со мной. Поэтому я и решил написать эту статью, в которой расскажу подробно о этих числах и как их использовать для обучения нейронных сетей. Сразу скажу, что я не прорабатывал все необходимые формулы для работы с такими числами, так как был занят своим языком программирования, это лишь идея, а не готовая реализация.Для того, что бы полностью понять о чём пойдёт речь в статье, нужно иметь знание о строении простых feedforward нейронных сетей.Предположим нужно обучить feedforward нейронную сеть имея некую обучающую выборку, в которой есть примеры того, что подаётся на вход нейронной сети и что ожидается получить на выходе. Для такого случая можно написать функцию, назовём её fitness (как в генетическом алгоритме), на вход такой функции даётся нейронная сеть и обучающая выборка, а функция возвращает число от 0 до 1, число соответствует тому, на сколько данная нейронная сеть обучена данной выборкой, где 0 - максимально не обучена, 1 - идеально обучена. Используя такую fitness функцию, нейронную сеть можно представить как математическую функцию у которой аргументы - это веса нейронной сети, а результатом является результат fitness функции применяемой к нейронной сети с данными весами и обучающей выборкой. Я начал размышлять "как найти максимум такой функции?". В свой голове я представил 3х мерный график функции с 2 аргументами и подумал, что если добавить условие что каждый вес будет ограничен каким либо конечным диапазоном возможных значений, то можно разделить этот график на две части, в одной части графика первый аргумент имеет одни значения из своего возможного диапазона, а вторая часть графика имеет все оставшиеся значения аргумента, затем проанализировать в какой части максимум больше, взять эту часть и делить её таким же образом, но уже опираясь на другой аргумент, после чего полученную в результате второго деления часть, снова нужно разделить на две части опираясь на первый аргумент. Такое деление на части нужно производить до тех пор, пока значения результата функции на полученном от делении участке, будут иметь слишком большие колебания. Любые аргументы из полученной части графика и являются подходящими весами. Для лучшего понимания, поясню вышесказанное на примере.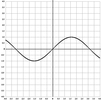

График функции y = sin xПредположим есть функция y(x) = sin x, x принадлежит множеству [-4, 4], нужно найти максимум, или значение очень близкое к максимуму, данной функции на данном участке. Разделим график на 2 части, в одной части x принадлежит множеству [-4, 0], во второй части x принадлежит множеству [0, 4], как видно на графике максимум находится во второй части, затем делим вторую часть на две части [0, 2] и [2, 4]. В какой-то момент в результате деления получится часть, в которых минимальное и максимальное значение функции очень близко к 1, например [pi * 999999 / 2000000, pi / 2], из этой части любой x будет приемлемым решением. Теперь о том как вышесказанное реализовать на практике. Однажды я сидел и смотрел в интернете научно-популярное видео, касалось оно космоса и в нём вскользь мелькнула информация о суперпозиции, в этот момент я подумал о числах которые не занимают определённую позицию, а находятся во многих местах одновременно. Например представить множество [0, 1], не как множество, а как число одновременно имеющее значение всех чисел из множества. Назовём такие числа "суперпозиционными". Результатом применения любой унарной операции к суперпозиционному числу, это суперпозиционное число, которое охватывает множество чисел, которые могут быть получены в результате применения унарной операции к любому числу из множества, которое охватывает исходное суперпозиционное число. Например: sin([-pi, pi]) = [-1, 1]. Результатом применения любой бинарной операции над суперпозиционными числами, это суперпозиционное число, которое охватывает множество чисел, которые могут быть получены в результате применения бинарной операции к двум любым числам из множеств, которые охватывают исходные суперпозиционные числа. Например: [-3, 6] - [-12, 7] = [-10, 18]. Вещественные числа так же можно представить в виде суперпозиционных как множество с одним числом, например [3, 3]. Что дают такие числа? Если есть некая функция с одним или несколькими неизвестными аргументами, но при этом значения этих аргументов ограничены каким либо конечным множество возможных значений, то подставив в качестве таких аргументов суперпозиционные числа, охватывающие собой множества возможных аргументов, можно узнать диапазон возможных значений функции. Вот как я придумал обучать простые feedforward нейронные сети:

создать нейронную сеть в которой все веса - суперпозиционные числа с множеством, которое ограниченно минимальным и максимальным значением веса
создать fintess функцию которая принимает указную нейронную сеть и обучающую выборку
уменьшить размер множества из суперпозиционного числа в одном весе в 2 раза, охватив либо половину множества с меньшими числами, либо с большими числами. Выбирается та половина, заменив на которую fitness функция даст большее значение. Если для обоих половин fitness функция выдаёт одинаковое значение, то выбирается случайная половина
выше указанные действия повторяются для каждого веса
выше указанные действия повторяются до тех пор, пока границы всех множеств суперпозиционных чисел в весах отличаются на определённое значение
заменить каждый вес на любое вещественное число из множества охватываемого суперпозиционным числом из соответствующего веса

Выше указанный алгоритм уже сейчас можно реализовать и опробовать на сколько он эффективен. Мне очень хотелось бы это сделать, но категорически не хватает времени. После того как я придумал данный алгоритм, я периодически о нём думал и понял, что у него есть очень весомая проблема - когда fitness функция будет производить анализ того на сколько нейронная сеть подходит для выборки, естественно что в процессе анализа, функция в том числе будет смотреть на сколько нейронная сеть подходит для каждого отдельного примера и может так получиться, что для каждого отдельного примера лучшие веса находятся в одном диапазоне значений, но самые подходящие веса для всей выборки в целом - в другом диапазоне. Для решения этой проблемы, мною был придуман ещё один вид чисел, а также новый алгоритм обучения который, как мне кажется, должен значительно увеличить вероятность выбора правильного множества чисел.Хотя как идея, суперпозиционные числа олицетворяют собой числа которые находятся одновременно в нескольких местах, по факту вышеуказанные алгоритм использует такие числа как олицетворение вещественного числа находящегося в неком промежутке, а в результате получаем промежуток в котором может быть результат действий производимого над числами. Одна из проблем такого подхода в том, что совершенно не учитываются вероятность получения каких либо значений в диапазоне чисел. Например: если есть некое число принадлежащее множеству [1, 2] и есть второе число принадлежащее множеству [4, 5], то если сложить два этих числа, получится число принадлежащее множеству [5, 7], но число 5 можно получить только если сложить 1 и 4, а для числа 6 существует бесконечное количество пар чисел, поэтому вероятность получения числа 6 выше, чем вероятность получения числа 5. Поэтому мною были придуман новый вид чисел, с помощью которых можно учитывать вероятности. Разумеется если взять некое бесконечное множество и некое неизвестное число гарантированно принадлежащее данному множеству, то вероятность того что это число будет равным некому заранее известному числу из этого множества, стремится к 0, поскольку множество бесконечно. Но вот что я придумал сделать, предположим есть множество [a, b] и есть некое случайное число x принадлежащее множеству, предположим что если разделить множество на n равных частей, то x имеет некую вероятность принадлежать одной из частей, для каждой части вероятность может быть различной. Предположим что есть функция f получающая номер части и возвращающая вероятность (от 0 до 1) того, принадлежит ли этой части число x. На основе функции f можно создать функцию f1, f1(x) = f(x) * n. При стремлении n к бесконечности, функция f1 возвращает значение, с помощью которого можно оценить вероятность того, что x находится в окрестностях некого числа. Если f1 возвращает значение 0, то считается, что вероятность существует, но она минимально возможная, а чем выше число, тем выше вероятность. Для создания нового вида чисел, я взял суперпозиционные числа и добавил к ним функцию f1. Характеристику числа, которую описывает функция f1 я изначально назвал концентрацией, но уже после того как я всё придумал, мне в подписки на youtube пришло два видео (первое, второе), в которых рассказывается о вероятности вероятностей и там такую характеристику называли плотностью, поэтому и я тоже буду называть её плотностью, а сами числа - плотностными. Для удобства в дальнейшем областью определения (какому множеству принадлежит x) функции в плотностных числах, будет множество [0, 1], а для получения плотности в конкретной точке, значение получаемое из функции, будет масштабироваться.С помощью таких плотностных чисел у fitness функции куда больше данных, для более качественной оценки весов нейронной сети. Выше я уже писал, что для уменьшения проблемы вызванной суперпозиционными числами, я придумал не только новый вид чисел, но и новый алгоритм обучения. Думая о том как решить проблему вызванную суперпозиционными числами, я понял что эта проблема очень сильно усугубляется тем, что все веса являются суперпозиционными числами и если в один момент во время обучения суперпозиционным числом будет только один вес, то это должно колоссально снизить проблему, а если заменить суперпозиционное число на плотностное, проблема должна ещё больше снизиться. И так, теперь только один вес является плотностным числом, а какими значениями заполнить все остальные числа? Случайными? Не очень мне такой подход нравиться и я решил, что можно в начале обучить нейронную сеть способом используемым с суперпозиционными числами, но вместо суперпозиционных чисел, использовать плотностные, а затем уже использовать новый подход. В результате финальный вариант алгоритма получился следующим:

создать нейронную сеть в которой все веса - плотностные числа с множеством, которое ограниченно минимальным и максимальным значением веса и с функцией y(x) = 1
создать fintess функцию которая принимает указную нейронную сеть и обучающую выборку
уменьшить размер множества из плотностного числа в одном весе в 2 раза, охватив либо половину множества с меньшими числами, либо с большими числами. Выбирается та половина, заменив на которую fitness функция даст большее значение. Если для обоих половин fitness функция выдаёт одинаковое значение, то выбирается случайная половина
выше указанные действия повторяются для каждого веса
выше указанные действия повторяются до тех пор, пока границы всех множеств плотностных чисел в весах отличаются на определённое значение
заменить каждый вес на любое вещественное число из множества охватываемого плотностным числом из соответствующего веса
заменить один вес на плотностное число, охватывающее множество ограниченное минимальным и максимальным значением веса
уменьшить размер множества из плотностного числа в одном весе в 2 раза, охватив либо половину множества с меньшими числами, либо с большими числами. Выбирается та половина, заменив на которую fitness функция даст большее значение. Если для обоих половин fitness функция выдаёт одинаковое значение, то выбирается случайная половина
выше указанное действие повторять до тех пор, пока границы множества плотностного числа в весе отличаются на определённое значение
заменить вес на любое вещественное число из множества охватываемого плотностным числом из веса
повторить 4 последних действия над каждым весом
если в результате последних 5-ти действий нейронная сеть стала более обученной, то повторить эти 5 действий ещё раз

Хотя и в суперпозиционных числах, и в плотностных числах может быть сколь угодно много отрезков возможных чисел (например: суперпозиционное число состоящее из 3 отрезков ([0, 1], [20, 40], [100, 101]) ), поскольку я эти числа использую только в контексте обучения нейронных сетей, то всё что я говорю ниже, относиться к плотностным числам которые состоят из 1 отрезка ограниченного 2-мя вещественными числами. В начале этой статьи я писал о том, что я не проработал все необходимые формулы и вот о каких формулах идёт речь. Если взять два плотностных числа [1, 2, y(x) = 1], [4, 5, y(x) = 1], то при сложении этих чисел получается число [5, 7, y(x) = 1 - |0.5 - x| * 2]. Откуда взялась функция y(x) = 1 - |0.5 - x| * 2? Я её вывел вручную и возможно она не верна, но даже если я не прав с формулой, то в любом случае при сложении двух плотностных чисел, в результирующем числе будет функция которая использует функции из слагаемых. Если в качестве функции активации нейронов использовать функцию y(x) = x, то даже в таком случае для обучения моим алгоритмом, нужно знать как складывать и перемножать 2 плотностных числа. С учётом того, что в результате сложения или перемножения двух плотностных чисел, формулы из 2-х исходных чисел будут храниться и в результирующем числе, то при увеличении количества нейронов и слоёв в сети, количество времени и памяти для обучения растёт экспоненциально. Однако есть одно но, для того чтобы узнать какая функция будет в результате сложения, необходимо знать только функции из слагаемых, т.е. в выражении [a1, b1, y1(x) = f1(x)] + [a2, b2, y2(x) = f2(x)] = [a3, b3, y3(x) = f3(x)], f3 не зависит от a1, b1, a2, b2, а зависит только от f1 и f2, если этим свойством обладает и произведение, то есть несколько оптимизаций с помощью которых можно значительно сократить скорость роста потребления памяти и времени во время обучения. Поскольку статья получилась и так не маленькой, а так же поскольку формулы для сложения и произведения пока не известны, рассказ об оптимизациях отложу на потом.P. S. Достаточно быстро я остановил разработку компилятора для моего языка, о котором была моя прошлая статья. Кратко о том по чему я это сделал - https://cine-lang.blogspot.com/2020/02/blog-post.html. После прекращения разработки, я начал разработку нового языка, у которого отсутствуют недостатки предыдущего. На момент написания статьи я реализовал новый язык, компилятор и стандартную библиотеку на 80%. Мне очень хочется закончить новый вариант своего языка программирования, а так же реализовать хотя бы, несколько из своих идей (когда закончу ЯП, хочу попробовать реализовать свой алгоритм сжатия изображений, аудио и видео). Но в последнее время жизнь складывается не очень (как в прочем и у многих), из-за совокупности нескольких факторов (включая пандемию), я потерял работу и если осенью я хотя бы грибами питался, то сейчас иногда приходиться и ролтоны есть. Из за того, что в данный момент я много времени трачу на поиск работы (подработок) и иногда еды, а так же из-за психологического давления того факта, что у меня нет средств к существованию, разработка языка продвигается медленно. Если я бы смог фокусироваться на разработке, то компилятор и стандартную библиотеку я закончил бы, скорее всего к концу февраля. Поскольку моя обычная зарплата не превышает 200 долларов США в месяц, даже незначительная финансовая помощь поможет мне значительно. По этому, прошу помощи у всех не равнодушных (на хабре есть кнопка "Задонатить"). Благодарю всех откликнувшихся.
===========
Источник:
habr.com
===========
Похожие новости:

Теги для поиска: #_algoritmy (Алгоритмы), #_matematika (Математика), #_mashinnoe_obuchenie (Машинное обучение), #_iskusstvennyj_intellekt (Искусственный интеллект), #_algoritmy (алгоритмы), #_mashinnoe (машинное), #_ii (ии), #_matematika (математика), #_nejroseti (нейросети), #_nejronnye_seti (нейронные сети), #_algoritmy (
Алгоритмы
), #_matematika (
Математика
), #_mashinnoe_obuchenie (
Машинное обучение
), #_iskusstvennyj_intellekt (
Искусственный интеллект
)

Профиль ЛС

Ответить на тему

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы

Текущее время: 22-Ноя 18:17
Часовой пояс: UTC + 5