[Занимательные задачки, Математика, Научно-популярное] Задача уровня «nightmare»: 4 случайные точки на сфере
Автор
Сообщение
news_bot ®
Стаж: 7 лет 6 месяцев
Сообщений: 27286
Мне очень понравился разбор задачи от 3Blue1Brown, выкладываю конспект для тех, кто любит изящные решения математических задач в читабельном виде.
Математическая олимпиада им. Уильяма Лоуэлла Патнема (William Lowell Putnam Mathematical Competition) — математическая олимпиада для студентов бакалавриата, обучающихся в университетах (колледжах) США и Канады. Вдохновителем олимпиады был Уильям Лоуэлл Патнем, американский юрист и банкир. Проводится Математической ассоциацией Америки ежегодно с 1938 года. Денежными призами награждаются пять лучших университетских команд (приз $25 000 за первое место) и двадцать пять студентов, лучших в личном зачете (приз $1000 за первое место).
— Википедия
Длится олимпиада два раза по 3 часа, всего 12 задач по 10 баллов за каждую. Средний балл, который набирают студенты — 1 или 2. Рассмотрим одну из самых сложных задач из этой олимпиады.

Выберем 4 случайные точки на сфере. Какова вероятность что центр сферы будет внутри тетраэдра, образованного этими точками?
Рассмотрим двумерный вариант этой задачи.

Рассмотрим 3 случайные точки на окружности. Какова вероятность, что центр окружности будет внутри треугольника?
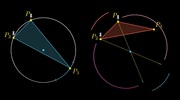
Можно закрепить две точки и поиграться с третьей. Легко заметить, что есть определенная зона, проекции закрепленных точек относительно центра, внутрь которой должна попасть третья точка, чтобы выполнилось условие. Окружность тем самым разделяется на 4 части. Вероятность попадания третей точки в дугу, равна отношению длины дуги к длине окружности. Какова длина дуги?

Вероятность колеблется от 0 до 0,5 в зависимости от расположения первых двух точек.
Какова средняя вероятность?
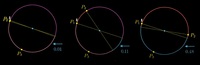
Зафиксируем первую точку и поиграемся со второй. Вероятность будет меняться от 0 до 0,5, то есть средняя вероятность будет 0,25.
Решение задачи для окружности и трёх точек — 25%.
Можно ли перенести такой подход на сферу и 4 точки?
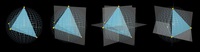
Фиксируем три точки и играем с четвертой. Нарисуем проекции фиксированных точек относительно центра и плоскостями разделим сферу на 8 частей.
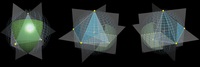
Центр сферы будет находиться внутри тетраэдра, если четвертая точка попадает на зеленый сферический треугольник, который находится «напротив» зафиксированных точек относительно центра. Каков средний размер зеленой секции?
//Дальше не придумали, импровизируй.
Можно вернуться к двумерному случаю и подумать откуда взялась 1/4. Откуда 4?
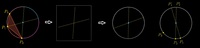
Можно перейти от 3 случайных точек на окружности к другой задаче. Выберем два случайных диаметра. Потом для каждого диаметра бросим монетку, выбирая тем самым, где будет точка Pi, с какого конца диаметра. Потом случайно выберем третью точку на окружности.
А потом еще хитрый ход.
Давайте сначала выберем случайным образом третью точку, а потом случайно выберем два диаметра. У нас будет 4 варианта размещения точек P2 P1:

Но только один из этих 4 вариантов содержит решение, когда центр окружности внутри треугольника:

Какую бы мы ни выбирали рандомную начальную позицию третей точки и двух диаметров, только один из вариантов содержит центр окружности внутри треугольника:

То как мы переформулировали задачу:
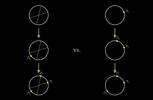
Со сферой получается 8 вариантов выбора точек, после того, как зафиксирована первая точка и выбраны три диаметра:
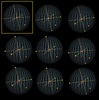
Только 1 из 8 удовлетворяет условию, что центр сферы внутри тетраэдра:

Ответ: 1/8
- Хардкорная линейная алгебра здесь: Capturing the Origin with Random Points: Generalizations of a Putnam Problem
- Все задачи олимпиады 1992 года: The 53rd William Lowell Putnam Mathematical Competition
Saturday, December 5, 1992
Извините, данный ресурс не поддреживается. :(
===========
Источник:
habr.com
===========
Похожие новости:
- [Научно-популярное, Физика] Рекогносцировка местности
- [Научно-популярное, Космонавтика, Астрономия] Японские ученые показали частички грунта с астероида Рюгу
- [Научно-популярное, Космонавтика] Тестовый запуск тяжелой ракеты. Запуски года: 106 всего, 15 от России
- [Читальный зал, Научно-популярное, Физика] Как древние шумеры повлияли на значение скорости света, и почему Великая Французская Революция не смогла им помешать
- [Занимательные задачки, Математика, Визуализация данных, Научно-популярное] Бесполезный паттерн в полярных координатах, открывающий полезное свойство простых чисел
- [Производство и разработка электроники, Научно-популярное, Транспорт] Лаборатория полупроводников Audi (перевод)
- [Научно-популярное, Космонавтика] Россия возобновляет испытательные полеты «Ангары» в третьей миссии. NSF
- [Научно-популярное, Физика] Первый в истории турнир по квантовым шахматам выиграл исследователь Amazon
- [Научно-популярное, Физика] ЦЕРН открывает доступ к данным Большого адронного коллайдера
- [Робототехника, История IT, Научно-популярное, Транспорт] Сто лет истории беспилотных автомобилей (перевод)
Теги для поиска: #_zanimatelnye_zadachki (Занимательные задачки), #_matematika (Математика), #_nauchnopopuljarnoe (Научно-популярное), #_matematika (математика), #_zanimatelnye_zadachki (
Занимательные задачки
), #_matematika (
Математика
), #_nauchnopopuljarnoe (
Научно-популярное
)
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 26-Авг 08:02
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 6 месяцев |
|
|
Мне очень понравился разбор задачи от 3Blue1Brown, выкладываю конспект для тех, кто любит изящные решения математических задач в читабельном виде. Математическая олимпиада им. Уильяма Лоуэлла Патнема (William Lowell Putnam Mathematical Competition) — математическая олимпиада для студентов бакалавриата, обучающихся в университетах (колледжах) США и Канады. Вдохновителем олимпиады был Уильям Лоуэлл Патнем, американский юрист и банкир. Проводится Математической ассоциацией Америки ежегодно с 1938 года. Денежными призами награждаются пять лучших университетских команд (приз $25 000 за первое место) и двадцать пять студентов, лучших в личном зачете (приз $1000 за первое место).
— Википедия Длится олимпиада два раза по 3 часа, всего 12 задач по 10 баллов за каждую. Средний балл, который набирают студенты — 1 или 2. Рассмотрим одну из самых сложных задач из этой олимпиады.  Выберем 4 случайные точки на сфере. Какова вероятность что центр сферы будет внутри тетраэдра, образованного этими точками? Рассмотрим двумерный вариант этой задачи.  Рассмотрим 3 случайные точки на окружности. Какова вероятность, что центр окружности будет внутри треугольника?  Можно закрепить две точки и поиграться с третьей. Легко заметить, что есть определенная зона, проекции закрепленных точек относительно центра, внутрь которой должна попасть третья точка, чтобы выполнилось условие. Окружность тем самым разделяется на 4 части. Вероятность попадания третей точки в дугу, равна отношению длины дуги к длине окружности. Какова длина дуги?  Вероятность колеблется от 0 до 0,5 в зависимости от расположения первых двух точек. Какова средняя вероятность?  Зафиксируем первую точку и поиграемся со второй. Вероятность будет меняться от 0 до 0,5, то есть средняя вероятность будет 0,25. Решение задачи для окружности и трёх точек — 25%. Можно ли перенести такой подход на сферу и 4 точки?  Фиксируем три точки и играем с четвертой. Нарисуем проекции фиксированных точек относительно центра и плоскостями разделим сферу на 8 частей.  Центр сферы будет находиться внутри тетраэдра, если четвертая точка попадает на зеленый сферический треугольник, который находится «напротив» зафиксированных точек относительно центра. Каков средний размер зеленой секции? //Дальше не придумали, импровизируй. Можно вернуться к двумерному случаю и подумать откуда взялась 1/4. Откуда 4?  Можно перейти от 3 случайных точек на окружности к другой задаче. Выберем два случайных диаметра. Потом для каждого диаметра бросим монетку, выбирая тем самым, где будет точка Pi, с какого конца диаметра. Потом случайно выберем третью точку на окружности. А потом еще хитрый ход. Давайте сначала выберем случайным образом третью точку, а потом случайно выберем два диаметра. У нас будет 4 варианта размещения точек P2 P1:  Но только один из этих 4 вариантов содержит решение, когда центр окружности внутри треугольника:  Какую бы мы ни выбирали рандомную начальную позицию третей точки и двух диаметров, только один из вариантов содержит центр окружности внутри треугольника:  То как мы переформулировали задачу:  Со сферой получается 8 вариантов выбора точек, после того, как зафиксирована первая точка и выбраны три диаметра:  Только 1 из 8 удовлетворяет условию, что центр сферы внутри тетраэдра:  Ответ: 1/8
Извините, данный ресурс не поддреживается. :( =========== Источник: habr.com =========== Похожие новости:
Занимательные задачки ), #_matematika ( Математика ), #_nauchnopopuljarnoe ( Научно-популярное ) |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 26-Авг 08:02
Часовой пояс: UTC + 5
