[Занимательные задачки, Математика, Визуализация данных, Научно-популярное] Бесполезный паттерн в полярных координатах, открывающий полезное свойство простых чисел
Автор
Сообщение
news_bot ®
Стаж: 7 лет 11 месяцев
Сообщений: 27286
Началось всё с обсуждение на математическом StackOverflow: Meaning of Rays in Polar Plot of Prime Numbers
«Недавно я начал экспериментировать с gnuplot и быстро сделал интересное открытие. Я построил все простые числа ниже 1 миллиона в полярных координатах, так что для каждого простого p (r, θ) = (p, p). Ничего особенного не ожидал, просто пробовал. Результаты впечатляют».

Если посмотреть на простые числа ниже 30000, можно увидеть спиральный узор.

Для сравнения — тот же график с наложенными на него числами, кратными 3 и 7. Штрихи выделены желтым цветом, кратные 3 и 7 — зеленым и красным соответственно.

Что действительно интересно, так это поведение при увеличении диапазона. Кратные данного числа кажутся спиралевидными по той же схеме в бесконечность, но простые числа начинают образовывать лучи группами по 3 или 4.

По сравнению с числами, кратными 3 и 7:

Связаны ли эти закономерности с теорема о простых числах? Являются ли эти лучи тем же явлением, что и диагональные линии в Скатерти Улама?
В ответ на объяснение Грега Мартина я решил добавить еще пару графиков. Чтобы понять, почему они актуальны, прочтите его ответ.
(г, θ) = (n, n), n∈N


Для начала можно поиграться с полярными координатами и рассмотреть все точки с целочисленными координатами: (1,1) (2,2)…
Получаем Архимедову Спираль:

Если исключить все числа, кроме простых, то получаем спиральную галактику с пробелами:

«Отдаляясь» мы можем увидеть направленные во все стороны лучи, по большей части в группах по 4 штуки:

Спирали можно посчитать, их 20 штук:

А лучей 280:

Если брать все числа, а не только просты, то спирали поровнее и их 44:

При самом близком рассмотрении у нас 6 спиралей:

Все числа, кратные 6 образуют одну ветку:

Остальные рукава спиралей 6к+1, 6к+2 и тд. Почему так? Потому что 6 примерно равно (полному обороту) 2ℼ (6.28318530718). Эта маленькая разница создает иллюзию единой кривой.
Если оставить только простые числа, останется только две спирали (6к+1 и 6к+5):

6 — почти полный круг, 44 — еще более точное приближение (44/2ℼ ≈ 7 полных кругов)
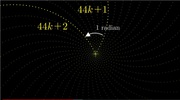
Только для простых чисел остается 20 рукавов (44к+1, 44к+3, 44к+5...). Функция Эйлера φ (44) = 20.

710/2ℼ ≈ 113. (113,00000959)

Для простых чисел будут пробелы:

Чем дальше отдаляемся, тем отчетливее проявляется кривизна всей структуры.
710=71*5*2. Это объясняет группировку по 4 луча (5) и «отломанные зубцы расчески» (71):

Функция Эйлера φ (710) = 280.
По теореме Дирихле, простые числа равномерно распределятся по рукавам.
Вывод
Играясь с визуализацией, можно наткнуться на а) принцип Дирихле б) на приближения числа ℼ (и цепные дроби) в) дойти до функции Эйлера.
Спиралевидная форма — это артефакт, связанный с совпадением с четным числом радианов.
Ролик с русской озвучкой:
Извините, данный ресурс не поддреживается. :(
P.S.
Еще работы по простым числам:
- Bounded gaps between primes. (By Yitang Zhang, 2014)
- Primes in tuples I (By DANIEL A. GOLDSTON, JÁNOS PINTZ, and CEM Y. YILDIRIM, 2009)
Цепные дроби от Савватеева:
Извините, данный ресурс не поддреживается. :(
Алексей Савватеев «Все о записи чисел»:
Извините, данный ресурс не поддреживается. :(
===========
Источник:
habr.com
===========
Похожие новости:
- [Производство и разработка электроники, Научно-популярное, Транспорт] Лаборатория полупроводников Audi (перевод)
- [Научно-популярное, Космонавтика] Россия возобновляет испытательные полеты «Ангары» в третьей миссии. NSF
- [Научно-популярное, Физика] Первый в истории турнир по квантовым шахматам выиграл исследователь Amazon
- [Научно-популярное, Физика] ЦЕРН открывает доступ к данным Большого адронного коллайдера
- [Робототехника, История IT, Научно-популярное, Транспорт] Сто лет истории беспилотных автомобилей (перевод)
- [Научно-популярное, Космонавтика] SpaceShipTwo не завелся
- [Криптография, Математика, Научно-популярное] Математический гений в криптографии: от сцитала до RSA
- [Научно-популярное, Космонавтика] Спутник радиовещания. Запуски года: 105 всего, 41 от США
- [Научно-популярное, Космонавтика] Исследователи нашли в Солнечной системе сеть «гравитационных шоссе»
- [Анализ и проектирование систем, Разработка систем связи, Научно-популярное, Физика, DIY или Сделай сам] Как данные передаются по радио?
Теги для поиска: #_zanimatelnye_zadachki (Занимательные задачки), #_matematika (Математика), #_vizualizatsija_dannyh (Визуализация данных), #_nauchnopopuljarnoe (Научно-популярное), #_matematika (математика), #_zanimatelnye_zadachki (
Занимательные задачки
), #_matematika (
Математика
), #_vizualizatsija_dannyh (
Визуализация данных
), #_nauchnopopuljarnoe (
Научно-популярное
)
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 15-Янв 12:00
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 11 месяцев |
|
|
Началось всё с обсуждение на математическом StackOverflow: Meaning of Rays in Polar Plot of Prime Numbers «Недавно я начал экспериментировать с gnuplot и быстро сделал интересное открытие. Я построил все простые числа ниже 1 миллиона в полярных координатах, так что для каждого простого p (r, θ) = (p, p). Ничего особенного не ожидал, просто пробовал. Результаты впечатляют».
 Если посмотреть на простые числа ниже 30000, можно увидеть спиральный узор.  Для сравнения — тот же график с наложенными на него числами, кратными 3 и 7. Штрихи выделены желтым цветом, кратные 3 и 7 — зеленым и красным соответственно.  Что действительно интересно, так это поведение при увеличении диапазона. Кратные данного числа кажутся спиралевидными по той же схеме в бесконечность, но простые числа начинают образовывать лучи группами по 3 или 4.  По сравнению с числами, кратными 3 и 7:  Связаны ли эти закономерности с теорема о простых числах? Являются ли эти лучи тем же явлением, что и диагональные линии в Скатерти Улама?
В ответ на объяснение Грега Мартина я решил добавить еще пару графиков. Чтобы понять, почему они актуальны, прочтите его ответ. (г, θ) = (n, n), n∈N   Для начала можно поиграться с полярными координатами и рассмотреть все точки с целочисленными координатами: (1,1) (2,2)… Получаем Архимедову Спираль:  Если исключить все числа, кроме простых, то получаем спиральную галактику с пробелами:  «Отдаляясь» мы можем увидеть направленные во все стороны лучи, по большей части в группах по 4 штуки:  Спирали можно посчитать, их 20 штук:  А лучей 280:  Если брать все числа, а не только просты, то спирали поровнее и их 44:  При самом близком рассмотрении у нас 6 спиралей:  Все числа, кратные 6 образуют одну ветку:  Остальные рукава спиралей 6к+1, 6к+2 и тд. Почему так? Потому что 6 примерно равно (полному обороту) 2ℼ (6.28318530718). Эта маленькая разница создает иллюзию единой кривой. Если оставить только простые числа, останется только две спирали (6к+1 и 6к+5):  6 — почти полный круг, 44 — еще более точное приближение (44/2ℼ ≈ 7 полных кругов)  Только для простых чисел остается 20 рукавов (44к+1, 44к+3, 44к+5...). Функция Эйлера φ (44) = 20.  710/2ℼ ≈ 113. (113,00000959)  Для простых чисел будут пробелы:  Чем дальше отдаляемся, тем отчетливее проявляется кривизна всей структуры. 710=71*5*2. Это объясняет группировку по 4 луча (5) и «отломанные зубцы расчески» (71):  Функция Эйлера φ (710) = 280. По теореме Дирихле, простые числа равномерно распределятся по рукавам. Вывод Играясь с визуализацией, можно наткнуться на а) принцип Дирихле б) на приближения числа ℼ (и цепные дроби) в) дойти до функции Эйлера. Спиралевидная форма — это артефакт, связанный с совпадением с четным числом радианов. Ролик с русской озвучкой: Извините, данный ресурс не поддреживается. :( P.S. Еще работы по простым числам:
Цепные дроби от Савватеева: Извините, данный ресурс не поддреживается. :( Алексей Савватеев «Все о записи чисел»: Извините, данный ресурс не поддреживается. :( =========== Источник: habr.com =========== Похожие новости:
Занимательные задачки ), #_matematika ( Математика ), #_vizualizatsija_dannyh ( Визуализация данных ), #_nauchnopopuljarnoe ( Научно-популярное ) |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 15-Янв 12:00
Часовой пояс: UTC + 5
