[Алгоритмы, Go] Algorithms in Go: Sliding Window Pattern (Part II)
Автор
Сообщение
news_bot ®
Стаж: 7 лет 8 месяцев
Сообщений: 27286
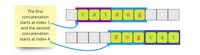
This is the second part of the article covering the Sliding Window Pattern and its implementation in Go, the first part can be found here.
Let's have a look at the following problem: we have an array of words, and we want to check whether a concatenation of these words is present in the given string. The length of all words is the same, and the concatenation must include all the words without any overlapping. Would it be possible to solve the problem with linear time complexity?
Let's start with string catdogcat and target words cat and dog.

How can we handle this problem? Unfortunately, the article name spoils all the intrigue — we can indeed apply the Sliding Window Pattern. Let's recap it base form:
- Iterate through items in the array till you fill the sliding window.
- Process the remaining items in the array in a step-wise fashion, and on each step check whether we fulfill the required condition. If the condition is fulfilled try to shrink the window from the left, and see whether the condition is still satisfied.
- To prepare for a new iteration, drop the leftmost item, and update the stats of the window if necessary.
- Repeat the loop till the array exhaustion.
Ok, how can we apply this algorithm to the problem at hand? Well, the array, in this case, is just our string, i.e. catdogcat.
Now, what is the window size in our case? As we need to find a substring that includes all the targeted words, its length must be at least equal to the combined length of the targeted words. What condition do we need to check at each step? A concatenation of all words is basically a permutation of all words. Therefore, by item in the array, we mean a substring of size equal to the size of a single word.
We iterate through each symbol in the string and constitute a new item with the last character equal to the symbol. At each step, we check whether the current item is equal to any of the target words. If we have matched all the words, we have found a required concatenation in the string. To track the number of matches we will have a running counter of matches with the initial value equal to the number of the target words. If the current item matches any of the required words we decrease the counter. Consequently, if the leftmost item that we are going to drop matches the target word, we increase the counter. When the counter goes down to zero, we have all the required matches.
However, a single match counter is not enough: if we have two occurrences of a word in the window, and we only need one, then we would (erroneously) decrease the counter twice. We need to check not only whether an item equals one of the target words, but also whether we already matched the word earlier. To do so, we calculate a frequency map of the targeted words, where words will be used as keys, and counts of needed occurrences as values. When an item matches a word, we decrease the frequency of the word. When the frequency goes down to zero, we have matched the word the required number of items. If we found one more occurrence of the word after that, we have too many "instances" of the word in the window, and the match wasn't useful. Therefore, we decrease the match counter, only when the item is present in the frequency map and still have a positive count in the frequency map.
We can visually represent the above algorithm in the following way:

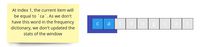

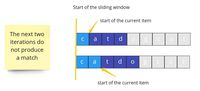

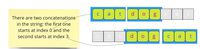
We continue the iteration in the same manner and find the second concatenation starting at index 3.
How can we represent the algorithm in the code?
We have two input arguments:
- string str representing the string in which we search the concatenations.
- slice of strings words that represents the target words.
We have slice of integers res that collects the starting indices of the concatenations as a single output.
We start with the initialization of the variables.
// the remaining number of matches
matches := len(words)
// start of the sliding window,
// not the start of the current item
var start int
freqs := make(map[string]int)
for _, word := range words {
freqs[word]++
}
wordSize := len(words[0])
var res []int
We iterate through all symbols in str and check whether the condition is satisfied.
for stop := wordSize - 1; stop < len(str); stop++ {
itemStart := stop + 1 - wordSize
item := str[itemStart : stop+1]
if freq, exists := freqs[item]; exists {
if freq > 0 {
matches--
}
freqs[item]--
}
if matches == 0 {
// shrink from the left
start = stop - len(words)*wordSize + 1
res = append(res, start)
}
// have not yet filled the window,
// no need to drop the leftmost item
if stop < len(words)*wordSize-1 {
continue
}
// prepare for the next iteration,
// i.e. accommodate space for the next item.
left := str[start : start+wordSize]
start++
if freq, exists := freqs[left]; exists {
if freq >= 0 {
matches++
}
freqs[left]++
}
}
Let's zoom some parts of the code.
if freq, exists := freqs[item]; exists {
if freq > 0 {
matches--
}
freqs[item]--
}
What is the purpose of this if condition? If the current frequency is zero we already filled all positions for the word in the window. If the frequency is less than zero we have more occurrences of the word in the current window than needed. In both such cases, we don't need any more occurrences of the word, therefore, the match wasn't useful and it shouldn't be counted.
left := str[start : start+wordSize]
start++
if freq, exists := freqs[left]; exists {
if freq >= 0 {
matches++
}
freqs[left]++
}
In the code snippet above, we do the reverse operation. If by dropping the leftmost item we losing a useful match, we increase the number of remaining matches.
After the iteration slice res contains starting positions of all possible concatenations of the words in the string. If there are no concatenations then res remains as an uninitialized slice.
What time complexity do we have? We iterate all the symbols in the string and on each iteration we slice a substring of size equal to the word size: O (N * M), where N is the length of the string, and M is the size of a word.
Here you can find the code and the tests.
===========
Источник:
habr.com
===========
Похожие новости:
- [Go, Разработка под Linux] Оптимизация размера Go-бинарника
- [Python, C++, Go] Сравним C++, JS, Python, Python + numba, PHP7, PHP8, и Golang на примере расчёта “Простое Число”
- [Информационная безопасность, Google Chrome, Расширения для браузеров, Браузеры] В бета-версии Chrome 88 включили Manifest V3, который изменит доступ расширений к данным
- [Игры и игровые приставки] Из-за ажиотажа при запуске Cyberpunk 2077 ненадолго слегли серверы Steam и GOG
- [Статистика в IT, IT-компании] Google опубликовала рейтинг запросов русскоязычных пользователей в 2020 году
- [Open source, Управление разработкой] Google меняет модель лицензирования операционной системы Fuchsia: теперь это полностью открытый проект
- [Open source, Софт, IT-компании] Google позволил сторонним разработчикам участвовать в работе над Fuchsia OS
- [Google Chrome, Браузеры] Chrome упрощает парольный менеджер
- [Разработка робототехники, Разработка под Arduino, DIY или Сделай сам, Электроника для начинающих] Как управлять BLDC по 25кВт в пике? Настройка контроллера Kelly KLS. Чтение состояния по UART
- [Научно-популярное, Космонавтика] Новая модель грузового корабля Dragon успешно прибыла на МКС
Теги для поиска: #_algoritmy (Алгоритмы), #_go, #_golang, #_go, #_algorithms, #_algoritmy (
Алгоритмы
), #_go
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 03-Ноя 02:57
Часовой пояс: UTC + 5
| Автор | Сообщение |
|---|---|
|
news_bot ®
Стаж: 7 лет 8 месяцев |
|
 This is the second part of the article covering the Sliding Window Pattern and its implementation in Go, the first part can be found here. Let's have a look at the following problem: we have an array of words, and we want to check whether a concatenation of these words is present in the given string. The length of all words is the same, and the concatenation must include all the words without any overlapping. Would it be possible to solve the problem with linear time complexity? Let's start with string catdogcat and target words cat and dog.   How can we handle this problem? Unfortunately, the article name spoils all the intrigue — we can indeed apply the Sliding Window Pattern. Let's recap it base form:
Ok, how can we apply this algorithm to the problem at hand? Well, the array, in this case, is just our string, i.e. catdogcat. Now, what is the window size in our case? As we need to find a substring that includes all the targeted words, its length must be at least equal to the combined length of the targeted words. What condition do we need to check at each step? A concatenation of all words is basically a permutation of all words. Therefore, by item in the array, we mean a substring of size equal to the size of a single word. We iterate through each symbol in the string and constitute a new item with the last character equal to the symbol. At each step, we check whether the current item is equal to any of the target words. If we have matched all the words, we have found a required concatenation in the string. To track the number of matches we will have a running counter of matches with the initial value equal to the number of the target words. If the current item matches any of the required words we decrease the counter. Consequently, if the leftmost item that we are going to drop matches the target word, we increase the counter. When the counter goes down to zero, we have all the required matches. However, a single match counter is not enough: if we have two occurrences of a word in the window, and we only need one, then we would (erroneously) decrease the counter twice. We need to check not only whether an item equals one of the target words, but also whether we already matched the word earlier. To do so, we calculate a frequency map of the targeted words, where words will be used as keys, and counts of needed occurrences as values. When an item matches a word, we decrease the frequency of the word. When the frequency goes down to zero, we have matched the word the required number of items. If we found one more occurrence of the word after that, we have too many "instances" of the word in the window, and the match wasn't useful. Therefore, we decrease the match counter, only when the item is present in the frequency map and still have a positive count in the frequency map. We can visually represent the above algorithm in the following way:      We continue the iteration in the same manner and find the second concatenation starting at index 3. How can we represent the algorithm in the code? We have two input arguments:
We have slice of integers res that collects the starting indices of the concatenations as a single output. We start with the initialization of the variables. // the remaining number of matches
matches := len(words) // start of the sliding window, // not the start of the current item var start int freqs := make(map[string]int) for _, word := range words { freqs[word]++ } wordSize := len(words[0]) var res []int We iterate through all symbols in str and check whether the condition is satisfied. for stop := wordSize - 1; stop < len(str); stop++ {
itemStart := stop + 1 - wordSize item := str[itemStart : stop+1] if freq, exists := freqs[item]; exists { if freq > 0 { matches-- } freqs[item]-- } if matches == 0 { // shrink from the left start = stop - len(words)*wordSize + 1 res = append(res, start) } // have not yet filled the window, // no need to drop the leftmost item if stop < len(words)*wordSize-1 { continue } // prepare for the next iteration, // i.e. accommodate space for the next item. left := str[start : start+wordSize] start++ if freq, exists := freqs[left]; exists { if freq >= 0 { matches++ } freqs[left]++ } } Let's zoom some parts of the code. if freq, exists := freqs[item]; exists {
if freq > 0 { matches-- } freqs[item]-- } What is the purpose of this if condition? If the current frequency is zero we already filled all positions for the word in the window. If the frequency is less than zero we have more occurrences of the word in the current window than needed. In both such cases, we don't need any more occurrences of the word, therefore, the match wasn't useful and it shouldn't be counted. left := str[start : start+wordSize]
start++ if freq, exists := freqs[left]; exists { if freq >= 0 { matches++ } freqs[left]++ } In the code snippet above, we do the reverse operation. If by dropping the leftmost item we losing a useful match, we increase the number of remaining matches. After the iteration slice res contains starting positions of all possible concatenations of the words in the string. If there are no concatenations then res remains as an uninitialized slice. What time complexity do we have? We iterate all the symbols in the string and on each iteration we slice a substring of size equal to the word size: O (N * M), where N is the length of the string, and M is the size of a word. Here you can find the code and the tests. =========== Источник: habr.com =========== Похожие новости:
Алгоритмы ), #_go |
|
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете голосовать в опросах
Вы не можете прикреплять файлы к сообщениям
Вы не можете скачивать файлы
Текущее время: 03-Ноя 02:57
Часовой пояс: UTC + 5
